Spaces
 |
Start with the idea of a space as a set of points with some structure. In algebraic geometry each point has coordinates and a metric, that is a distance between every two points. In topology we can have a looser structure between the points depending on the type of topology. |
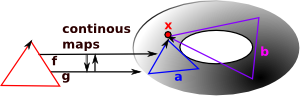
Topological spaces allow us to retain the concept of continuous maps between spaces, even in non-metric spaces.
Shape
Here we are concerned with shapes, when they are the same shape and the mappings between them.
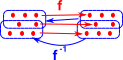
For example, continuous mappings as allow a toroid to be continuously mapped into a mug. It is like a sort of 'rubber geometry' where there are no absolute distances. |
 |
Determining Same Shape
There are different ways to 'equate' shapes such as homotopy equivalence and homeomorphisms.
We can use 'invariants': properties of topological objects which do not change under certain mappings.
- are they split into multiple parts?
- number of holes
- homology group
- homotopy group
Often we need to know if a shape can be continuously deformed into another shape. There are different types of continuous maps.
| For instance a Möbius band is homotopy equivalent to a non-twisted band but they are not homeomorphic. |  |
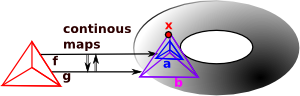
Homeomorphism
A homeomorphism is quite a strict form of 'same shape'. There is a 1:1 correspondence between points on the two shapes. A point is mapped to a point on the other shape and the mapping in the reverse direction takes it back to the original point. This is like an isomorphism with continuous mappings. |
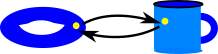 |
 |
As these are continuous mappings, points that are near to each other must be mapped to points that are also near to each other. |
The concepts of nearness and continuous mappings are defined more fully on the page here.
Homotopy Equivalence
A homotopy equivalence is a looser form of 'same shape' than a homeomorphism.
| There are continuous maps that are not allowed in a homeomorphism. For example, a line can be continuously contracted down to a point but that would not be allowed in a homeomorphism because the reverse mapping would not take every point back to itself. |  |
Therefore a homotopy equivalence is commonly used rather than a homeomorphism.
This allows more shapes to be considered the same. For example a Möbius band can be continuously deformed to a non-twisted band by first contracting it continuously to a circle and then continuously expanding it to a band.

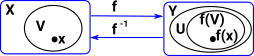
How this can homotopy equivalence be defined more precisely? We can't map every point in X to a point in Y and require an inverse map which brings the point back to where it started. |
 |
Continuity
So we need a way to make this continuity idea more precise.
Fibration - Line to Point Map Example
| To keep things simple, take the example of a line continuously retracted down to a point. |  |
 |
To see this, in its most general form, as a continuous map between topological spaces I have drawn the line consisting of representative points and open sets. |
For it to be a continuous map the preimage of an open set must be an open set. We don't want to have to make any arbitrary decisions about which open set to map back to, so the preimage is the open set around the whole line. |
 The red arrow is a map between open sets. |
This is the homotopy lifting property. When we look at more complicated examples (see fibration page) we will see structure between points being lifted to structure between open sets.
Homotopy Equivalence
If we continuously map every point in X to a point in Y and require an inverse map which brings the point back to where it started and do this in both directions we get a homeomorphism. But if we want a homotopy equivalence (shapes which can be continuously deformed into each other) then we only need a weaker requirement that this round trip and the identity maps are a homotopy. |
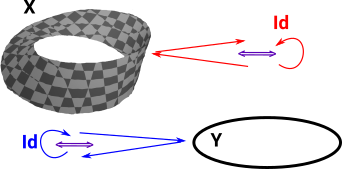 |
More about homotopy equivalence on the page here.
Homotopy
For comparison start with the idea of functional equality: if F(x)=G(x) for all x |
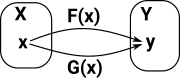 |
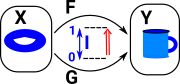 |
We need a weaker form of sameness to allow, say, a torus to be somehow the same shape as a cup. |
| Here the points F(x) and G(x) are different but both functions still cover the whole cup. |  |
Homotopy
 |
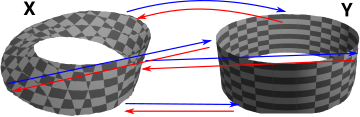
If we have two topological spaces X & Y with two continuous maps between them F & G then a homotopy is a continuous map between F & G. In order to see how this is related to the map between the cup and torus I have drawn a map from a third shape (in this case another torus). So as F continuously maps the G then the cup maps to the torus. |
We can move the continuous map forward from the functions to the domain so the functions are homotopic if:
where:
We can think of this as 'filling in' the gap between F and G so that we can take any path through it. |
 |
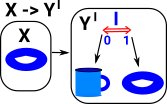 |
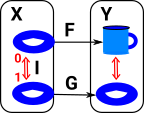
Or we can draw it in the codomain (currying) so that each element in X maps to I->Y. |
More about homotopy on page here.
In two dimensions it is relatively easy to determine if two spaces are topologically equivalent. We can check if they:
- are connected in the same way.
- have the same number of holes.
However, when we scale up to higher dimensions this does not work and it can become impossible to determine homeomorphism. There are methods which will, at least, allow us to prove more formally when topological objects are not homeomorphic.
These methods use 'invariants': properties of topological objects which do not change when going through a homeomorphism. Here we look at two types of invariants which arise from homotopy and homology.
HomotopyIt would take up too much space to properly explain the concept here so see this page for more details |
If 2 spaces are homotopy equivalent the fundamental groups are isomorphic. In homotopy we use equivalence classes between a circle and loops (which don't collapse) on the topological object that we are investigating. We can get further invariants by extending the circle to the surface of higher order n-spheres. We can then get algebraic structures (mostly groups) by investigating what happens when these loops are composed, the loops are generators of the group. In homotopy the order of these compositions can be significant, that is the groups are not necessarily abelian. |
HomologyIt would take up too much space to properly explain the concept here so see this page for more details |
In homology we don't just use n-spheres but every closed oriented n-dimensional sub-manifold. It also uses a different definition of equivalence classes where composition of loops commutes. This results in abelian groups. So we don't need to fix the basepoint. |
Example
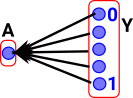
Are the two shapes on the right 'homotopy equivalent' ? Is there a continuous map between them in both directions? There is more about this example on the page here. |
 |
Topology on a Set
A topology on a set X is a collection Τ of subsets of X, called open sets satisfying the following properties:
- X and Ø are elements of Τ.
- Τ is closed under finite intersections.
- Τ is closed under arbitrary unions.
The requirements for the existence of of meets and joins correspond to the requirements for the existence of unions and intersections of open sets. Therefore these lattice structures can represent topologies.
| Lattice | Open Set | |
|---|---|---|
| invalid - every intersection should be an open set: |
| Venn Diagram | Topological Space (or not) | Lattice (frame) |
|---|---|---|
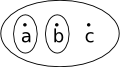 |
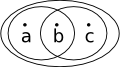
This is not a topological space because 'a' and 'b' are subsets but not the union of 'a' and 'b' | |
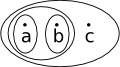 |
This is now a topological space because we have added the union of 'a' and 'b' | 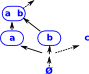 |
 |
This is not a topological space because 'ab' and 'bc' are subsets but not their intersection. |  |
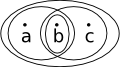 |
This is now a topological space because we have added 'b' | 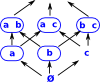 |
Note: Assume Ø is included in the above examples.
Topological Space
In many cases the concept of a metric space is unnecessary, however we still need the concept of 'nearness' and hence 'continuity'. 'Topological space' based on the 'topological open set' is the most general way we can do this. This allows us to define nearness purely using the concept of a subset.
Hausdorff Space
Hausdorff space is a bit more specific than general topological space. Space is Hausdorff if, in addition to being a topological open set, for any two points:
x1, x2![]() X there are disjoint open sets U1, U2 that contain x1and x2.
X there are disjoint open sets U1, U2 that contain x1and x2.
Basis
A basis is a subcollection B![]() = U
= U
where
- U is the open set
- B is the basis
 = a subcollection (subset) - I need to add the proper symbol for this.
= a subcollection (subset) - I need to add the proper symbol for this.
such that every element of U is a union of open sets in B.
Link between Topology and Logic
One way to visualise the link between topology and logic is to start with a Venn diagram. We can then map points in the Venn diagram to either true or false depending on whether they are in a given set. |
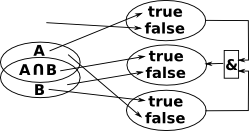 |
This is a nice way to link geometry, logic and topology.
see pages about:
Link between Topology and Category Theory
Presheaf
Fibre in Category Theory
See page here.
Slice Category
See page here.
Examples
Non-Geometric Examples
Sequences
Here the concept of 'nearness' comes from sequences that begin in the same way.
Denotional Semantics
Recursively Defined Structures
Further Information
see pages about: