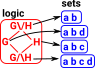
A set is a collection of things, which are called the elements of the set.
"an abstract set X has elements each of which has no internal structure whatsoever" - Lawvere.
In mathematics 'set' is a fundamental concept but there are different approaches that can be taken to it:
- There are various formulations of set theory. In, say the ZF formulation, everything is a set.
- Often we may look at set as a sort of minimal structure onto which we can add extra structure.
- In computing a set may be seen as a collection, like a list, where there are no duplicates and order is not important.
- There is a correspondence between set theory and second order logic.
Here we mostly treat set as a minimal structure, with the concept of set membership and subsets, onto which we can add other structures.
Concepts
| a ∈ A | The basic concept of set theory is set membership. This expression means that 'a' is an element of 'A'. |
Sets can be specified in various ways:
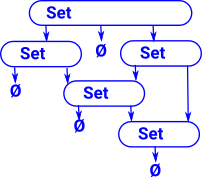
| {1,2,3} | We can list all the elements, that is, build up the set from nothing: Ø | |
| {n | n<4} | We can start with an existing set (in this case n - the set of natural numbers) and then apply constraints to it. |
Principle of Comprehension
If φ(x) is a property of object x then there exists a set whose elements have that property.
Equality
Set TheoryIn, say the ZF formulation of set theory, everything is a set.The elements of a set are themselves sets and their elements are sets. Its sets all the way down until we get to an empty set. Also an element cannot occur more than once in a set so a given set can't contain more than one empty set. An element can occur in more than one set but loops would allow paradoxes. This is a difference between set theory and type theory, the page here discusses the relationship between set theory and type theory. |
 |
Set + Structure
Inverse Functions
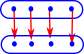
In general a function is not invertible, in that if we reverse all the arrows we don't necessarily get back to where we started. Bijective functions are invertible but reversing the arrows in injective and surjective functions gives something that is not a function.
| Lets look an example where we try to invert an surjective function. | |
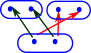
| If we try to invert this example some of the elements in the domain go to multiple elements in the codomain so this is not a total function. In category theory we can have arrows which are more general than functions so there would be some categories where this is valid but not the category of set. | 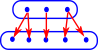 |
| So what is the closest we could get to this using ordinary functions? | 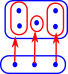 |
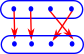
| Lets look an example where we try to invert an injective function. | |
| If we try to invert this example there is nowhere for the first two elements to go so this is not a total function. Again, in category theory we can have arrows which are more general than functions so there would be some categories where this is valid but not the category of set. | |
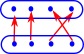
| So what is the closest we could get to this using ordinary functions? |  |
Proofs about Sets
A key part of mathematics is proofs.
In order to prove things about sets we need a logic layer underpinning it.
Proofs in Isabelle
Isabelle is a program known as a proof assistant. More about this program on this page.
In Isabelle sets are typed. All elements have the same type (say τ) and the set itself has the type τ set (the order of type constructors is reversed compared to many languages). A type variable a is written: 'a so a set of these is written: 'a set.
| Isabelle Notation | Meaning |
|---|---|
| a ∈ A | A is a member of B |
| a ∉ A | A is not a member of B |
| {} | empty set |
| UNIV | universal set |
| {a,b,c} | a finite set consisting of elements a,b and c |
| {x. P} | comprehension set of all elements that satisfy predicate P |
| {p*q | p q. p |
more complicated comprehension in this case all numbers which are the products of two primes. Could also be represented by: {x. |
| A |
A is a subset of B |
Set Membership
The Isabelle code (from this site) starts with two concepts:
- member (
 ) Membership is the key concept of sets. In Isabelle it is a binary operator which takes a element and a set and returns true if the element is a member of the set.
) Membership is the key concept of sets. In Isabelle it is a binary operator which takes a element and a set and returns true if the element is a member of the set. - Collect infers the members of a set from a predicate, this is known as set comprehension.
axiomatization Collect :: "('a => bool) => 'a set" -- "comprehension"
and member :: "'a => 'a set => bool" -- "membership"
where
mem_Collect_eq [iff, code_unfold]: "member a (Collect P) = P a"
and Collect_mem_eq [simp]: "Collect (λx. member x A) = A"
notation (HTML output)
member ("op ∈") and
member ("(_/ ∈ _)" [51, 51] 50) and
not_member ("op ∉") and
not_member ("(_/ ∉ _)" [51, 51] 50) |
The axioms show Collect and member as being some sort of inverse. that is, Collect allows us to compose a set and member allows us to decompose it.
In category theory a function a subobject classifier has the type: 'a set => bool.
Set comprehension is a construction that allows us to define a set by stating the properties of its members.
Mappings
Mappings, functions between sets are discussed on page here.
Subset
A![]() B means A is a subset of B
B means A is a subset of B
A![]() B iff
B iff![]() x
x![]() A :
x
A :
x![]() B
B
Subsets and Logic
There is a relationship between subsets and logic.
This can give rise to different set theories, for instance, constructive or intuitionistic logic gives rise to constructive set theory.
Intersection, Union and Venn Diagrams
IntersectionThe intersection of two sets is another set which contains the elements in both the original sets. |
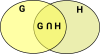 |
UnionThe intersection of two sets is another set which contains all the elements from original sets, if an element is in both the original sets then it is only included once, not twice. |
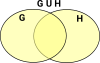 |
ComplementThis is everything not in the set. This has to be defined in terms of the universe under discussion. |
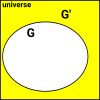 |
Cartesian Product
The Cartesian product of two sets is a set of pairs representing every combination of the two sets. This is a very general product that we can define regardless of whether multiplication is a valid operation for the elements of the sets being multiplied. So this type of product 'generates' a higher dimensional quantity. |
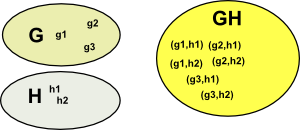 |
So what happens when we multiply two of these two dimensional quantities?
(g1,h1)(g2,h2) = ?
Perhaps it might generate a 4 dimensional quantity:
(g1,h1)(g2,h2) = (g1,h1,g2,h2)
Or we might be able to define a multiplication which would make this equivalent to complex number multiplication:
(g1,h1)(g2,h2) = (g1g2 - h1h2 , g1h2 + g2h1)
Or we may require a different definition,as an example, lets take the dihedral group D3, that we looked at on this page. We might represent any transform as a pair like:
(ma,ra)
Consisting of one reflection and one rotation, we can represent any element of this group by such a pair.
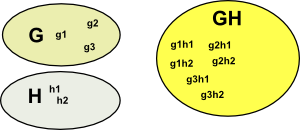
| Lets take another example, imagine that we have a group G and a subgroup H with elements g1,g2… and h1,h2… | 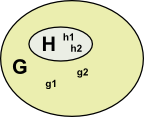 |
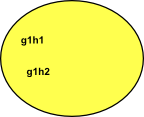
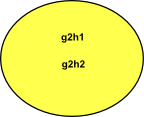
In this case we can now define multiplication as g1 H * g2 H = g1 g2 H
| g1 H | g2 H | g1 g2 H |
 |
 |
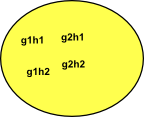 |
| left coset g1 of H | left coset g2 of H | left coset g1,g2 of H |
Product
If multiplying individual elements of the first set by elements of the second set is valid, then the product no longer needs to be represented by pairs, in this case the product contains the product of every combination of the two sets. If we are combining two groups then we may be able to use an external or internal product as described on this page.
Equivalence Relation
Generalisation of equality to set theory.
If two sets are exactly equal, this may not be all that interesting from a mathematical point of view. It is often more interesting when two sets are not identical but preserve some form of structure when mapping between them.
| type | category notation | |
|---|---|---|
| tighter | Equality | |
| Isomorphism | 1 = GF FG = 1 |
|
| Equivalence | 1 FG |
|
| looser | Adjunctions | 1 => GF FG => 1 |
Equivalence:
| Set Notation | Alternative Notation | Property |
|---|---|---|
| (a,a) |
a |
Reflective |
| (a,b) |
a |
Symmetric |
| (a,b) |
a |
Transitive |
Sequence in a set
A function from N (the set of positive integers) to the set.
In other words each element of the set is assigned a number.
Notation:
{an}n=1∞
Indexing sets
An index set is a set used to label the elements of another set using a surjective function.
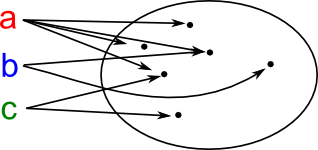
An alternative approach is to attach a name to each element of a collection of sets.
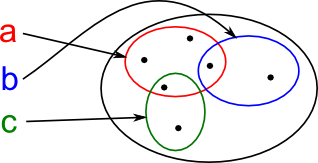
Notation:
{aα}α∈A
Related Topics
Next
Mappings, functions between sets are discussed on page here.