Maths - Lattice

In this context a lattice is a mathematical structure with two binary operators: \/ and /\.

The lattice structure arises in algebras associated with various branches of mathematics including logic, sets and orders. These branches of mathematics tend to use different names and notations for corresponding concepts as follows:

Lattice	Logic	Set	Order
	=>		≤
	<=>	=	=
top T	true	universe	empty meet /\Ø
bottom _|_	false	Ø	empty join \/Ø
/\ meet	conjunction,and	intersection	greatest lower bound glb infimum inf
\/ join	disjunction,or	U union	least upper bound lub supremum sup

So we can approach lattices in different ways:

• We can define them using the concept of 'order', that is, as a partially ordered set (poset).
• We can define them using algebraic identities.

This lattice structure can be visualised as a diagram with nodes and lines between them, this diagram is called a Hasse diagram. This has some similarities to a graph structure however the lines in a lattice structure have a notion of 'ordering' and there will be a highest node at the top and a lowest node at the bottom.

A big application of mathematical lattices is when factoring is involved somehow.

Categorisation of Lattices

	If a lattice represents a completely ordered set (a>b or a<b is valid for any two elements) then the lattice is just a vertical line.
N5	M5	O6
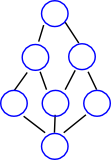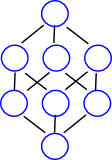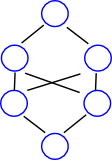L7	23	P6

Lattice and Partially Ordered Sets

A lattice is a partially ordered set in which any two elements have a least upper bound and a greatest lower bound.

For partially ordered sets:

• the join operation represents the least upper bound of an arbitrary set of elements.
• the meet operation represents greatest lower bound of an arbitrary set of elements.

A partially ordered set where both the join and the meet of any two elements always exist is a lattice

• A partially ordered set where the join of any two elements always exists is a join-semilattice.
• A partially ordered set where the meet of any two elements always exists is a meet-semilattice.

For n-ary relations:

• An n-ary relation on a set A is a subset of Aⁿ
• The inverse r^¬ of a binary relation on A is specified by <a,b>r iff <b,a>r
• The relational product r o s of two binary relations r,s on A is given by <a,b>r o s iif for some c: <a,c>r <c,b>s.

Completeness

If a poset/lattice has completeness properties then it can be described as an algebraic structure.

The presence of certain completeness conditions allows us to regard the formation of certain suprema and infima as total operations of an ordered set. It turns out that in many cases it is possible to characterize completeness solely by considering appropriate algebraic structures in the sense of universal algebra, which are equipped with operations like \/ or /\. By imposing additional conditions (in form of suitable identities) on these operations, one can then derive the underlying partial order exclusively from such algebraic structures.

	completeness	requires negation operation
lattice
semilattice
Heyting algebra		'pseudo complement'
Boolean algebra		'not' operation

Algebra of Lattice

An important algebra is a lattice, it has two operations:

• meet /\
• join \/

identities:

identity	meet	join
commutativity	x /\ y = y /\ x	x \/ y = y \/ x
associativity	(x /\ y) /\ z = x /\ (y /\ z)	(x \/ y) \/ z = x \/ (y \/ z)
idempotency	x /\ x = x	x \/ x = x
absorption laws	x \/ (x /\ y) = x	x /\ (x \/ y) = x

there are also distributive laws which may, or may not, apply for a particular lattice.

identity
distributive /\ over \/	x /\ (y \/ z) = (x /\ y) \/ z
distributive \/ over /\	x \/ (y /\ z) = (x \/ y) /\ z

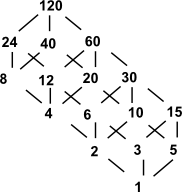
Example - Factorising integer

As an example of a lattice we will look at factorising an integer, in this case 120. The following table the columns represents an integer we are trying to factorise and the row represents the the integer we are trying to factorise by. The entry in the table is a boolean value where '' represents true and blank represents false depending on whether row is a factor of column:

Is-a-factor-of	1	2	3	4	5	6	8	10	12	15	20	24	30	40	60	120
1	√	√	√	√	√	√	√	√	√	√	√	√	√	√	√	√
2		√		√		√	√	√	√		√	√	√	√	√	√
3			√			√			√	√		√	√		√	√
4				√			√		√		√	√		√	√	√
5					√			√		√	√		√	√	√	√
6						√			√			√	√		√	√
8							√					√		√		√
10								√			√		√	√	√	√
12									√			√			√	√
15										√			√		√	√
20											√			√	√	√
24												√				√
30													√		√	√
40														√		√
60															√	√
120																√

So the function 'is-a-factor-of' has a type signature of (int,int) -> boolean

We can convert the above 'is-a-factor-of' table into an 'is-direct-factor-of' table, So since 4 is a factor of 8 we don't need to include the factors of 4 as direct factors of 8:

Is-direct-factor-of	1	2	3	4	5	6	8	10	12	15	20	24	30	40	60	120
1		√	√		√
2				√		√		√
3						√				√
4							√		√		√
5								√		√
6									√				√
8												√		√
10											√		√
12												√			√
15													√
20														√	√
24																√
30															√
40																√
60																√
120

We can put this in terms of a diagram:

	divisors
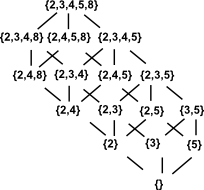	prime powers

From this diagram we can create two operations [type signature of (int,int) -> int] called meet and join. In meet we go upwards in the diagram, from each of the nodes representing the operands, to find the first common node where they first meet. In join we go downwards in the diagram, from each of the nodes representing the operands, to find the first common node where they first join.

Meet /\

least common factor

\/	1	2	3	4	5	6	8	10	12	15	20	24	30	40	60	120
1	1	2	3	4	5	6	8	10	12	15	20	24	30	40	60	120
2	2	2	6	4	10	6	8	10	12	30	20	24	30	40	60	120
3	3	6	3	12	15	6	24	30	12	15	60	24	30	120	60	120
4	4	4	12	4	20	12	8	40	12	60	20	24	60	40	60	120
5	5	10	15	20	5	30	40	10	60	15	20	120	30	40	60	120
6	6	6	6	12	30	6	24	30	12	30	60	24	30	120	60	120
8	8	8	24	8	40	24	8	40	24	120	40	24	120	40	120	120
10	10	10	30	40	10	30	40	10	60	30	20	120	30	40	60	120
12	12	12	12	12	60	12	24	60	12	60	60	24	60	120	60	120
15	15	30	15	60	15	30	120	30	60	15	60	120	30	120	60	120
20	20	20	60	20	20	60	40	20	60	60	20	120	60	40	60	120
24	24	24	24	24	120	24	24	120	24	120	120	24	120	120	120	120
30	30	30	30	60	30	30	120	30	60	30	60	120	30	120	60	120
40	40	40	120	40	40	120	40	40	120	120	40	120	120	40	120	120
60	60	60	60	60	60	60	120	60	60	60	60	120	60	120	60	120
120	120	120	120	120	120	120	120	120	120	120	120	120	120	120	120	120

Join \/

greatest common denominator

/\	1	2	3	4	5	6	8	10	12	15	20	24	30	40	60	120
1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
2	1	2	1	2	1	2	2	2	2	1	2	2	2	2	2	2
3	1	1	3	1	1	3	1	1	3	3	1	3	3	1	3	3
4	1	2	1	4	1	2	4	2	4	1	4	4	2	4	4	4
5	1	1	1	1	5	1	1	5	1	5	5	1	5	5	5	5
6	1	2	3	2	1	6	2	2	6	3	2	6	6	2	6	6
8	1	2	1	4	1	2	8	2	4	1	4	8	2	8	4	8
10	1	2	1	2	5	2	2	10	2	1	10	2	10	10	10	10
12	1	2	3	4	1	6	4	2	12	3	2	12	6	4	12	12
15	1	1	3	1	5	3	1	1	3	15	5	3	15	5	15	15
20	1	2	1	4	5	2	4	10	2	5	20	4	5	20	20	20
24	1	2	3	4	1	6	8	2	12	3	4	24	6	8	12	24
30	1	2	3	2	5	6	2	10	6	15	5	6	30	10	30	30
40	1	2	1	4	5	2	8	10	4	5	20	8	10	40	20	40
60	1	2	3	4	5	6	4	10	12	15	20	12	30	20	60	60
120	1	2	3	4	5	6	8	10	12	15	20	24	30	40	60	120

Diagrams

see Hasse diagram.

Relationship Between Poset and Algebra

We can represent a poset as a diagram:

meet: where two branches meet above we have a meet /\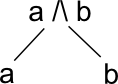
join: where two branches meet beneath we have a join \/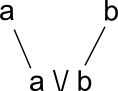

Warning: different sources somtimes reverese the way that /\ and \/ are used so I am not sure which is the best standard to use?

Birkhoff's theorem

All distributive lattices can be represented by sets as follows:

distributive lattice	set	poset	boolean
join operation \/	union U	least upper bound (supremum)	or
meet operation /\	intersection	greatest lower bound (infimum)	and

examples:

• the Boolean lattice defined from the family of all subsets of a finite set has this property.
• any finite topological space has a lattice of sets as its family of open sets.

 

Complemented lattice

In the mathematical discipline of order theory, a complemented lattice is a bounded lattice in which every element a has a complement, i.e. an element b satisfying a \/ b = 1 and a \/ b = 0.

An orthocomplementation on a bounded lattice is a function that maps each element a to an "orthocomplement" a^¬ in such a way that the following axioms are satisfied:

• Complement law: a^¬ \/ a = 1 and a^¬ \/ a = 0.
• Involution law: a^¬¬ = a.
• Order-reversing: if a ? b then b^¬ ? a^¬.

Boolean algebras are a special case of orthocomplemented lattices

EuclideanSpace

home

Prerequisites

• On this page we look at maps or morphisms between objects.

  On this page we look at graphs.

Related Subjects

• Proof and Proof
• Implementing Lattice using FriCAS/Axiom computer algebra system.

Set Symbols

Intersection

Meet

Category Theory