Concepts
Enumerable Sets
| A set Σ is enumerable iff its members can be listed (possibly infinite list) off in some numerical order with every member appearing on the list (allowing repetitions). | 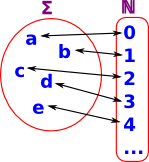 |
Effectively Enumerable
A set Σ is effectively enumerable iff either Σ is empty or there is an effectively computable function that computes it.
theorem
The set W of all effectively enumerable sets of natural numbers is itself enumerable.
theorem
Some sets of numbers are not effectively enumerable and hence not effectively decidable.
theorem
There is an effectively enumerable set of numbers K such that its complement
| K |
theorem
Some effectively enumerable sets of numbers are not decidable.
Effectively Computable
A one-place total function f: Δ->Γ is effectively computable iff there is an algorithm which can be used to calculate, in a finite number of steps, the value of the function for any given input from the domain Δ.
Characteristic Function
The characteristic function of the numerical property P is the one-place function
cP: N->Ω such that if n is P, cP(n)=true else cP(n)=false.
(see subobject classifier in category theory/topos).
The characteristic function of the two-place numerical relation R is the two-place function cR: (N,N)->Ω such that if m is R to n,then cR: (m,n)=true else cR: (m,n)=false.
Effectively Decidable
A property/relation is effectively decidable iff there is an algorithmic procedure that a suitable programmed computer could use to decide, in finite number of steps, whether the property/relation applies to any appropriate given items(s).
or
A numerical property/relation is effectively decidable iff its characteristic function is effectively computable.
Numerical Domain
The numerical domain of an algorithm Π is the set of natural numbers n such that, when the algorithm Π is applied to the number n as input, then the run of the algorithm will eventually terminate and deliver some number as output.
theorem
W is an effectively enumerable set of numbers iff it is the numerical domain of some algorithm Π.
