The sheaf structure is a powerful idea that goes across many mathematical subjects and therefore it can be approached from different directions:
|
|
|
 |
|
Cop-> Set |
|
|
|
As a way to relate global structure to local structure.
Sometimes it is relatively easy to take apart some structure but how to we reverse that and construct a large structure from a small fragment.
As a Generalisation of a Fibre Bundle.
As a pre-sheaf with some additional axioms.
hX = homC(_,X) : Cop-> Set
see representable
As a Way to Attach Data to a Space
| Perhaps a helpful way to start to characterise a sheaf is as a way to attach data to a space. This gives us way to relate various data, for instance, it might allow us to go between 'local' data and 'global' data. | |
| In this case the 'space' might be a topological space or something similar and the 'data' is sets and mappings between them. | |
| A topological space (discussed on this page) gives a concept of 'closeness' even if this can't be measured by a numerical distance. So, in the diagram on the right, the red box is a topological space and 'b' may be closer to 'a' than 'c'. A sheaf (or presheaf) extends this relationship to the blue structures. In this way we can start to see how 'local' data may be related to 'global' data. |  |
A topological space is quite restrictive and there may be ways to loosen the requirements to work with other spaces. Topological spaces are discussed on the pages here. |
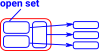 |
Pre-sheafA topology consists of open sets with some structure and we need to relate this to sets and functions between them. This is done using a contravarient functor. The arrows in the topological space are injective and they map to sets and functions between them in the opposite direction. |
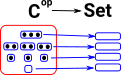 |
These relations need to obey certain axioms and so we need to make this all more precise.
| from ncatlab | Idea of presheaf: Given a small category C of “primitive objects”, we can think of a functor F:Cop ->Set as being a more complex object built out of primitive objects. |
Fibre With StructureThe page about fibre bundles here shows how reversing a map between sets gives some interesting structures. Here we extend that idea. A restriction of 'u' to 'v' is notated resv,u : F(u)->F(v) s|v restricts s to v see Wiki |
 |
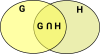
Example - SubsetsIn order to try to find a simple example lets say that A and B are sets and B is a subset of A. If we look at it in terms of logic we can say that A implies B so the arrow goes from A to B. When we look at the elements on the right it is simplest to show it as an injective function. |
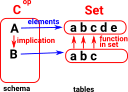 |
Example - Graph and Simplical Complexes |
 |
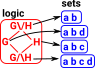
The category theoretic approach is to investigate objects, in this case graphs, in terms of the arrows (morphisms) between objects. So we are probing it from the outside.
The internal view can be more intuitive, especially to newcomers to category theory, so here we are relating the internal and external views to help with intuition. A graph is similar to a category theory diagram, but is weaker, in the sense that there is no requirement for compositions and identity loops to exist. Although category theory diagrams and graphs are different in this way here we see how they interact so we can get some information about the graph from its category theory diagram.
To do this we need to work with all the arrows from an object so we need to have the concept of a homset (see page here)
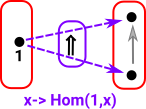
As a start with this approach we want to probe the red object on the right: To do this start by 'probing' it with arrows from a graph with only one vertex and no edges. All the possible arrows from the single vertex object form a homset. This homset is a set (where the elements are arrows) so we can use our set theoretic intuition on it. This set has one object for every vertex in the object. |
 |
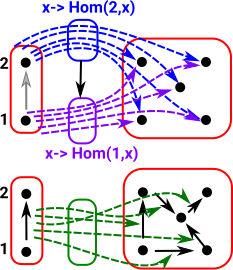 |
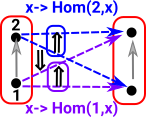
Now we need to 'probe' the edges. We can do this with an arrow from a graph with a single edge between two vertices. The bottom part of the graph on the left shows arrows (green) to each edge. So this time we have a homset which gives the number of edges. However, the mapping of the edges needs to play well with the mapping of the vertices (top part of diagram).
Similarly with vertex 2
|
It is easier to see this contravarience from a simpler diagram. If 'F' is given we can derive 'h' from 'g' by composing with 'F' but we can't derive 'g' from 'h'. So if we want to get the usual functions in set we need to start with Grfop A contravarient functor of the form Cop->set occurs in other structures and is called a presheaf as described on page here. |
 |
This graph object that we are using to 'probe' another graph object is known as a representable object in Grf (see Yoneda lemma page). This representable object is a graph with two vertices and an arrow between them. |
- More about relating category theory to set theory view of graphs on page here.
- We can extend this example from graphs to simplicial sets as described on page here.
Example - Relational Databasesee this page. |
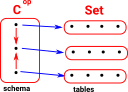 |
Example - Equalitiessee this page.
|
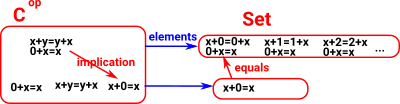 |
Example - Cubical Type Theorysee this page.
|
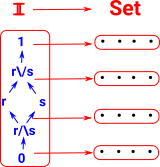 |
Sheaf from Presheaf
So far we have seen that, in order to have some nice properties, the presheaf must conform to the restrictions of being a contravarient functor. To be a sheaf we need to add two more restrictions, locality and gluing, then we can get the posibility of relating the local and global properties.
First we need to explain the terminology of 'covering' and a 'section' before we define locality and gluing:
Covering
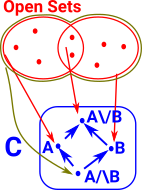
| from Wiki | A cover (or covering) of a set U is a collection of subsets of U whose union is all of U. |
| from ncatlab | A cover on an object U in a category C is a collection of morphisms A specification of a collection of covers for each object of the category, subject to some compatibility condition, makes a coverage on C |
| For instance, in this diagram, the 3 subsets: U1, U2 and U3 contain all the elements. | 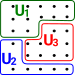 |
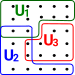 |
It is valid for these subsets to overlap, so that elements may be contained in many subsets, provided that each element is in at least one. |
Section
| from ncatlab | A section of a morphism f:A->B in some category is a right-inverse: a morphism g:B->A such that f•g:B->A->B equals the identity morphism on B. |
An assignment of values from each of the stalks that is consistent with the restrictions. Sections can be:
If all local sections extend to global sections the sheaf is called flabby/flasque (don't have interesting invariant's). |
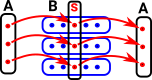
global section 's'. |
Sheaf Locality and Gluing
| from ncatlab | A presheaf on a site is a sheaf if its value on any object of the site is given by its compatible values on any covering of that object. |
A sheaf is a presheaf that satisfies the following two additional axioms (see Wiki):
LocalityIf U is an open covering of an open set U , and if s , t |
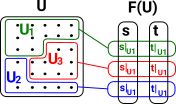 |
GluingIf U is an open covering of an open set U, and if for each |
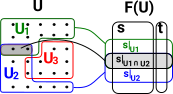 |
Where the notation used is:
- s | U i means s restricted to U i
- s is a section of the space over U
Topology
What if we start with sets which already have some structure? The diagram on the right is intended to show a morphism between partial orders. So the blue arrows represent ≥ and the arrow 'ab' means b ≥ a. The red arrows show the morphism between the partial orders and these all need to play nicely together. |
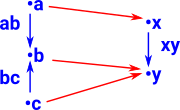 |
So how can this morphism be reversed? The diagram on the right is the best I can do although somehow it doesn't seem completely correct, for instance it seems to imply that c ≥ a whereas the original diagram above doesn't imply that. In order to be consistent this morphism needs to be a local homeomorphism which is a function between topological spaces that preserves local but not necessarily global structure. |
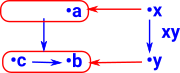 |
Local and Global StructuresThe interesting thing is that this is dividing the structure into 'local' structure and 'global' structure. It seems natural to have morphisms that preserve global structure but may compress local structure. This does give a morphism that is reversible and we get a fibre bundle with some extra structure. However, that's not what we want for a sheaf, what we want is a morphism that preserves local structure but may compress global structure. |
|
Local HomeomorphismIn order to be reversible this morphism needs to be a local homeomorphism, as in the example on the right, here the local structure is preserved. |
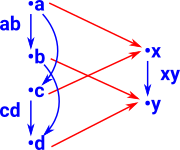 |
Reversing this morphism gives a fibre structure, as described on this page, but with additional structure. Now the local structure inside the xy type (on the right of the diagram) maps to the same structure between the family of types. This is also a comma category as described on this page. |
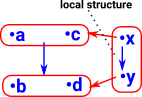 |
Here I have just rotated the above diagram by 90 degrees just to show in the same way we did with fibres. So each element x,y of x->y indexes a type. |
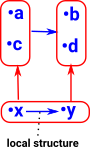 |
SectionIf we have a subset (subtype?) of the indexing type then this translates to a subset of the type family. |
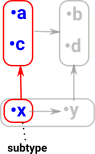 |
So far we have only described only part of what a sheaf is. What is described so far is a presheaf, this gives us lots of copies of the local structure. Making a presheaf into a sheaf allows us to glue these local structures together to form a more interesting structure.
Presheaf in Category Theory
A 'presheaf' category is a special case of a functor category (see page here). It is a contravarient functor from a category 'C' to Set.
Since it is contravarient it is usually written:
Cop->Set
or
SetCop
So we have a functor from a category to the category of sets. This sends objects to sets and arrows to functions in a way that plays well with the objects. In category theory we don't tend to look inside objects but in set theory we look inside sets. S how can we define these morphisms? In order to work with sets it needs to preserve something to do with subsets.
There is more about presheaves on the page here.
Presheaf on a Topological Space
A sheaf tends to be on a topological space.
We can get to this concept by replacing the sets discussed above with 'open sets' (more about open sets on page here).
We can have a presheaf of any structure 'A' on a topological space 'X'.
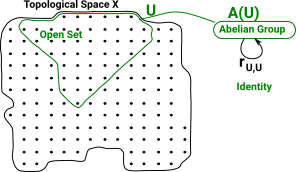
A presheaf of sets 'A' on 'X' is valid but it does not give much structure to relate the open sets. Something with an abelian group structure for example (such as vectors) gives us more structure to work with. More about open sets on page here.
A presheaf of abelian group 'A' on 'X' assigns to each open set U and that assigns to each pair U rU,V : A(V) -> A(U) |
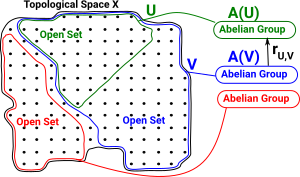 |
in such a way that rU,U = 1 (identity map) |
 |
| rU,VrV,W = rU,W (composition) | 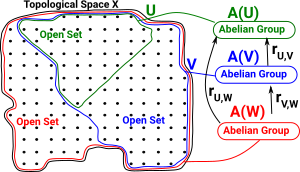 |
Presheaf in Category Theory
In category theory terms:
- X is a topological space
- A presheaf of abelian groups on X is a contravariant functor from the category of open subsets of X and inclusions to the category of abelian groups.
Let C=Top(X) the category whose objects are the open subsets of X. C can be represented as a poset of open sets in a topological space with the morphisms being inclusion maps.
In the same way as for fibres we usually reverse the arrow so that it is a contravarient arrow from Cop to Set: |
 |
A presheaf on a category C is a functor F : Cop-> Set
For instance a presheaf can be a contravariant functor from the category Top(X) to the category Ab of Abelian groups (which may also have more structure).
Sheaves are discussed from a category theory point of view on the page here.
Developing Fibre Bundle ApproachThe page here introduced fibre bundles. For example, where there is a family of types indexed by elements of another type. |
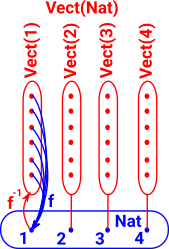 |
| The type families in fibre bundles are disjoint. One way to extend that concept is to allow an overlapping type family. |  |
| open sets | simplectical complex | |
In some cases we can convert between open sets and simplices. see Wikipedia articles: |
 |
 |
Sheaf and Co-Sheaf
Allow us to translate between physical sources of data and open sets or simpicies.
| sheaf | Co-sheaf |
|---|---|
| vertex weighted | hyperedge weighted |
| vertex has non-trvial stalk. | toplex has non-trvial stalk. |
| All restrictions are zero maps | All extensions are zero maps |
| The resulting sheaf is flabby | The resulting cosheaf is coflabby |
Diagrams
We can think of this in a combinatorics way. The relations are shown more clearly in an attachment diagram here. This shows subset relations with the arrows going from lower dimension to higher dimension. |
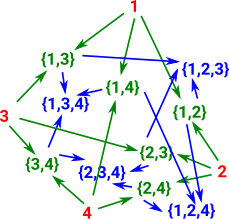 |
A sheaf assigns some data spaces to the attachment diagram above. In this case reals (ℜ) - A sheaf of vector spaces. Each such set is called a stalk over the simplex.
|
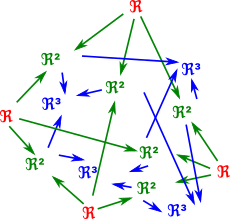 |