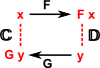Category theory is a very generalised type of mathematics, it is considered a foundational theory in the same way that set theory is.
Category theory concerns mathematical structures such as sets, groups topological spaces and many more. We can also go to a higher level such as the category of small categories.
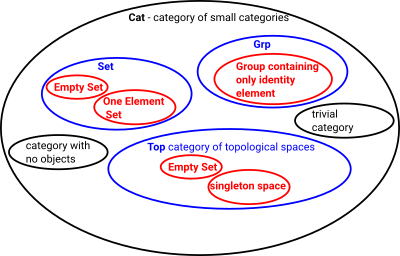 |
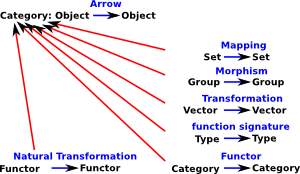
A diagram intended to give some indication of the sort of objects that may be in a category. |
The above diagram shows various of these categoies (in blue) their structures are explored by looking at their objects (in red) and the arrows between them. The objects are not elements, as is set theory, but are complete structures such as a 'group containing only identity element'. More important are the arrows between these objects, these tell us about the structure of the category.
There are various ways to start to characterise category theory:
- As an algebra of functions, that is where the elements are functions and the operation is composition. This algebra turns out to be a monoid of functions. (There is a relationship to λ-calculus which is also a calculus for manipulating functions)
- As a directed graph (graph as in graph theory) where objects are nodes in the graph and morphisms are edges (arrows) in the graph.
Category theory abstracts away from these details to a much more higher order theory.
We will discuss these in more detail later but first I would like to get more of an intuitive feel for how these mathematical structures can help us understand things about other (possibly all?) mathematical structures.
In some ways category theory is complementary to set theory. Set theory builds up from elements of the set to define a structure, we may have variables which allow us to abstract their properties, we may then get general laws like the associative rule. I am not using these words in a very technical way here, I am just just trying to paint a picture of the set theoretical approach as building up a set from the inside by understanding its components (its elements).
In contrast to this category theory works from the outside to infer the general laws of a given algebra. Category theory does not tend to consider the concept of an 'element', instead an 'object' in category theory is a complete algebra, it is like a 'black box' where we cant see directly inside it but we can only know its external properties.
We don't make arbitrary choices about what may be inside an object, this limits what we can know about it, so in general we can only describe an object 'upto isomorphism'. However we can learn a surprising amount about a category in this way, like axioms such as the associative rule, and this is done in a very general way which means that what we learn about one category can be applied to other categories. This allows us to abstract to an even higher level which gives us structures that apply across a very wide part of mathematics.
Although we can't see inside an object we can have specific sub-algebras (I am still using terminology very loosely here) such as initial and terminal objects and products and sums, these are determined by universal properties as described on this page.
The way that we determine the external properties of an object is by using morphisms between the objects (usually the term 'morphism' is generalised to 'arrow'). The properties arise from the way that these arrows compose and whether various paths commute.
Category Theory is a generalisation of other branches of mathematics which starts with noticing that many mathematical entities have mappings between them that preserve structure. This is generalised to a category with arrows between objects. |
 |
I have tried to illustrate this in the case of sets (imperfectly) on the diagram on the right. At the top I have put more general concepts (we will explain initial and terminal objects later), lower down I have put more specific concepts. In category theory we do not model down to the internal elements of an algebra, so we don't model functions/mappings as in the bottom part of the diagram. Our functions are only modeled as structure preserving morphisms between whole objects. However, from this, we can still infer a lot about the internal structure. We model the structure 'up to isomorpism'. |
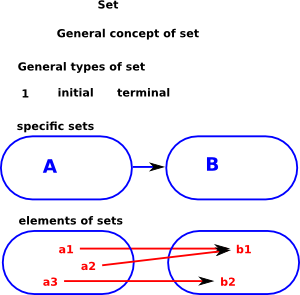 |
So the implied message here is that there is a link between the external properties of an algebra and its internal structure.
| In the diagram we have a 3 layer hierarchy, at the top we have a node representing all sets. Below that we have various types of sets such as, the empty set, a set with one element, a set with two elements and so on. Below that we have the elements of the sets. | 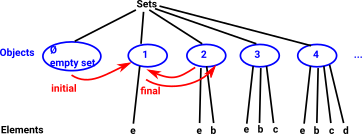 |
Category theory concentrates on the middle of these 3 layers. That is, we do not derive properties by looking inside at the elements of the sets, instead we derive properties by looking at the mapping between sets.
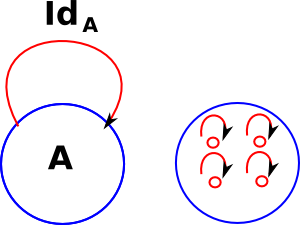
Although category theory tends to look at external properties and so would not look at equality of objects inside the category. Category theory does however look at equality of arrows under certain circumstances. So, for instance, IdA means an arrow from A back to itself that does not change the object (Id does not represent a permutation). So the blue circle on the left is the category theory diagram and the blue circle on the right is an equivalent set theory diagram. |
 |
| It is often required that a diagram commutes, that is, following the arrows A->B->D is equal to A->C->D although it is not always the case that a diagram commutes and sometimes we may require that a diagram commutes 'up to isomorphism'. | 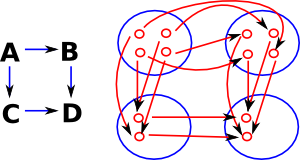 |
Foundational Theory
Category theory is a candidate for a theory that describes all of mathematics, that is it gives a possible way to axiomise mathematics. Another candidate for the axiomation of mathematics is is set theory, in particular a variant of set theory Zermelo–Fraenkel (ZFC) which avoids paradoxes. Category theory is also very useful for clarifying things which appear more complicated using other approaches, it also has lost of practical applications in computer science, so I think it is a worthwhile subject of study.
| Set Theory | Category Theory |
|---|---|
| Set theory tends to look inside a set, at subsets and so on, to give us structure. | Category Theory theory tends to look outside the category, at the arrows, so the structure comes from the way that it interacts with other categories. |
Approximate analogs of set theory concepts:
| Set Theory | Category Theory |
|---|---|
| element of a set | terminal object |
| empty set | final object |
| injective functions, subobject |
monomorphism(monic), if: m: M->X then X is a subobject of M |
| surjective functions | epimorphism(epic) |
| inverse function | isomorphism |
| intersection | pullback |
| function space | exponential |
| indexed family (special case of function) | cone (limit) |
Associative Axiom
To illustrate how category theory analyses mathematical structures, from the outside rather from the inside, lets look at how we would specify that a given structure obeys say: the associative axiom. In set theory we would specify:
a * (b * c) = (a * b) * c
That is we specify the rule in terms of 3 arbitrary elements inside the set, here denoted a,b and c. First a notational change to move to a more functional notation, we rewrite
a * b as μ(a,b) where μ is a mapping G²-›G which gives:
μ(a,μ(b,c)) = μ(μ(a,b),c)
now we rearrange to get the arbitrary elements a,b,c as operands on the right:
(μ•(id×μ))(a,b,c) = (μ•(μ×id))(a,b,c)
so now we can cancel out a,b,c and write the equation purely in terms of functions rather than what the functions are operating on, that is we 'lift' the equation from elements to functions:
μ•(id×μ) = μ•(μ×id) where:
|
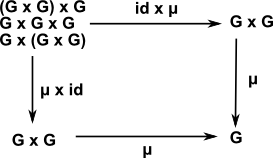 |
This has done two things:
- We are now working purely in terms structure preserving functions (known as functors, morphisms or arrows)
- We are now specifying the properties purely in terms of external effects rather than internal structure.
This allows us to generalise structures, for instance, groups are usually defined over sets but what if we want to define a group over some other mathematical structure? We need to separate the 'group structure' from the set it is being defined over, these methods may provide a way to do that.
We can also categorise other axioms such as commutivity and identity element (see group objects page).
Summary so far
Category theory looks at structures that occur in various branches of mathematics and analyses them in terms of 'objects' and 'arrows'. These objects are themselves whole mathematical 'structures'. They are not objects in the 'object oriented programming' sense, we don't tend to instantiate them, we tend to work with general abstract structures, however they do have some similarities to objects. A group over a set, for example, has an analogy to 'data' which could correspond to the set and 'procedures' which could correspond to the binary operation on the set. So these objects 'feel' like more than passive data.
Category theory tends to be more interested in the arrows than the objects, that is we don't tend to look inside the objects but treat them more like a 'black box' and think of the abstract properties of the structures and their relationship to each other.
A category is a graph with a rule for composing arrows to give another arrow. So a category has a structure of its own, a meta-structure, with rules for combining the arrows.
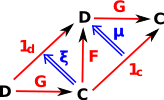
Interpretation of Arrow Diagrams
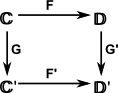 |
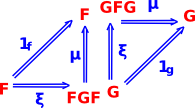
Typically in category theory we work with a lot of diagrams like the one on the left (the diagram itself is a mathematical structure called a graph). The nodes on the graph are mathematical objects such as sets, groups and so on. The 'arrows' may represent functions, morphisms and so on and are known as functors. For more about this see 'functors' described on this page. A diagram like this may specify structure by requiring that it commutes. That is, going from C to D' via D we get the same as going via C', so if we apply the functor F to G' we get the same as G applied to F'. The interpretation of a diagram like the one on the left may depend on context. For example we may say that a certain property is true if the diagram commutes, upto equivalence or possibly isomorphism (see comparing objects section below for different ways that objects can be 'equal'). So what does that mean? If c F' ( G(c)) and going the other way round the diagram we would get: F ( G'(c)) so, we are saying, these two things must be isomorphic for the property to be true. In other circumstances we may only require some looser condition for the property to be true. In this diagram there are no loops, a loop would indicate an infinite category unless we impose some additional limitation (an equation or a supplementary diagram) such as the requirement that FG = 1c with the diagram below. |
|||||||||
So there are many ways that we can compare objects, if there are arrows like the diagram on the left, which are valid upto isomorphism, then this implies that C is isomorphic to D. So, starting at C, and applying F then G we get an object that is isomorphic to C. The concatenation of F and G is the identity functor 1c
|
||||||||||
Concrete Categories
A concrete category is a category that looks like a category of “sets with extra structure”, that is a category of structured sets. (ref nLab)
We can start exploring category theory by representing specific (concrete) mathematical subjects in category theory terms. When we do this we loose the specifics of the subject and abstract to pure structure. We can then work in terms of categories without being concerned with unnecessary details. When required we can move back to a specific category and apply our results to a different area of mathematics.
In the table below I have listed the corresponding objects and arrows for various concrete categories:
| Category | Objects | Objects are | Arrows |
|---|---|---|---|
| Set | Sets | pure sets | functions |
| Grf | Graph | set + structure | |
| Grp | Groups | set + structure | morphism |
| Rng | Ring | set + structure | morphism |
| Vec | Vector space over a field | set + structure | linear transformation |
| Top | Topological space points in a topological space |
set + structure | continuous map smooth paths in spacemodule homotopy |
| Integers | n x m matrices | ||
| elements of a preorder | p <= g | ||
| functors | natural transformations | ||
| Cat | Category | pure structure | functor |
Not all concrete categories consist of a set with additional structure, however all categories are isomorphic to such categories.
So in the category of categories we have taken this to a higher level of abstraction, now the objects are themselves categories.
Sets to Categories
When learning about category theory it is hard to understand categories as shown in the graph above, the level of abstraction seems so high that it is hard to give any meaning to anything.
It is simplest to start with sets, in this case the objects are sets and the arrows are functions between those sets, in this case we are on familiar ground and it is relatively easy to give a physical meaning to the diagram.
A next step might be Grf, a category of graphs. The individual objects are graphs, that is sets with functions to themselves (endomap), so an object is now a set+structure. The arrows now preserve, not only some relationship between the elements of the sets but also relate the structure.
Some of the other categories above (Grp, Rng, Vec and Top) are also sets + structure so we can work out arrows between these objects.
We can now abstract further, perhaps our objects might be statuctures-over-sets-with-structures or statuctures-over-statuctures-over-sets-with-structures and so on. Eventually the sets become so deeply buried that we can make the leap from set+structure to pure structure.
In the category Cat the objects themselves are categories and there is no underlying set.
Graph Categories
Grf is a category of graphs, these have a bit more structure than sets and so will allow us to explore the relationships between objects which are sets+structure. I find it helpful to adapt the diagrams as bit, to get us started, so that we can include some of the normally hidden structure beneath. This is just to get us started, we won't always do this as the nature of category theory is to abstract as much as possible. Lets start with sets, which are perhaps the simplest objects, because they don't have the structure of operations like multiplications and additions.
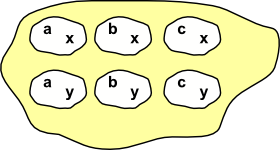 |
Sets may just be any set of elements, or some or all of these sets may themselves be sets (and these inner sets may also contain sets and so on). Also these elements may all have a common type or not. So we could show the structure inside the set instead of representing them as single characters. |
 |
In the case of structures like groups with a group operation then we could show that, perhaps by combining with a Cayley graph. |
Elements
x |
||
| 1 | -> | X |
- An element of a set is a member of the set
- An element of a graph is a loop in the graph
- An element of automation is a fixed point
- An element of a fiber bundle is a section
Combining Functions, Mappings and Functors
Here we will talk about functions although the same issues apply to functors.
| Conventional Maths Notation |
Haskell Notation |
|
|---|---|---|
| a function of one variable | y |
f: X -> Y |
| a function with multiple input parameters | y |
f: X -> X -> Y |
| a function with multiple output parameters | f(y1 |
In category theory we tend to avoid defining functors in terms of their elements like x and y. Instead we define f by its properies.
We can combine two, or more, compatible functions in various ways to create new functions. Such as:
- Functional Composition
- Currying
- Carteasian Product
- Sum
Functional Composition
In this case we apply the output of one function 'f' to the input of the next function 'g' like this: g(f(x)) the combined function can be written like this: f•g and applied to an element like this: (f•g)(x) Of course the output of f must be compatible with the input of g (the same type and number of parameters). |
Functional composition in category theory is shown on the arrow diagrams by the head of g going to the same node as the tail of f. So functional composition is the basis of category theory. |
Currying
A function which takes multiple parameters can be converted into a chain of functions each with a single parameter. In programming terms, when a function is called its parameters are 'bound' to their reqired values, so we just 'bind' the parameters one at a time.
Carteasian Product of Functions
We can combine two compatible functions to get their product. Imagine that we have two functions:
y = f(x)
b = g(a)
Then we can take a function in terms of the carteasian products of the inputs and outputs:
(y,b) = (f×g)(x,a)
Alternativly we can define this using arrow diagrams (see poduct on universal properies page)
We can also combine two compatible functions to get their sum (coproduct)
Comparing objects
When comparing objects it is often more interesting when two sets are not identical but preserve some form of structure when mapping between them.
![]()
| relative strength | type and category notation | description | ||||
|---|---|---|---|---|---|---|
| tightest | Equality | C and D are the same in these terms | ||||
| Isomorphism 1d = GF FG = 1c |
There must be an arrow and inverse between the objects and when composed these give the identity map for every element. | |||||
| Equivalence 1d FG |
For equivalence there is a arrow in both directions between the two objects. It is not necessary that GF and FG are the identity elements but they must be isomorphic to the identity elements. |
|||||
| loosest |
|
For adjunctions there is a arrow in both directions between the two objects. It is not necessary that GF and FG are the identity elements but only that they have natural transformations to the identity elements. FG is unit (does not change object - injective followed by surjective) but GF does change object (surjective followed by injective). Like equivalence but in one direction. Alternative definition: there is an isomorphism: |
These various ways to compare categories are explained in more detail on this page.
Universal Properties
Here we look at properties of categories that are common across all concrete categories from different branches of mathematics. As discussed earlier we are trying to find the properties of a category from its external interactions and universal properties give us a way to do this. In particular we may be looking for unique arrows (morphisms) that have some particular property.
In universal properties there is a unique isomorphism somewhere, this gives the 'best' of such a property.
Examples of universal properties are:
They occur in pairs which are the dual of each other.
More discussion of universal constructions on this page.
Monoid
A monoid is a semigroup with an identity element.

The axioms required of a monoid operation are those required of morphism composition when restricted to the set of all morphisms whose source and target is a given object.
A monoid is a category with a single object.
Given a monoid (M,*), one can construct a small category with only one object and whose morphisms are the elements of M. The composition of morphisms is given by the monoid operation *.
Likewise, monoid homomorphisms are just functors between single object categories. In this sense, category theory can be thought of as an extension of the concept of a monoid. Many definitions and theorems about monoids can be generalised to small categories with more than one object.
Notation
| notation | example | meaning | |||
|---|---|---|---|---|---|
| A |
Map / Morphism / Function / arrow / functor between mathematical structures that relates or preserves the structures in some way. May be injection, surjection or bijection (injection can be specifically indicated see below) | ||||
| a |
A function in terms of elements of the structures a |
||||
| A function that is valid if all the functions drawn as solid lines are valid | |||||
| injective morphism (embedding) | |||||
| canonical map - map of G onto factor group G/H where H is a normal subgroup of G | |||||
|
Natural Transformation |
More notation on this page.