Maths - Functor - Homset

Hom Functors

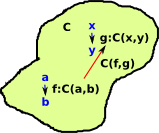
Given a category with objects such as: a,b...x,y f:C(a,b) represents all the morphisms from a to b. g:C(x,y) represents all the morphisms from x to y. We can now take this up one level. A hom functor C(f,g) represents all the functors from f to g.

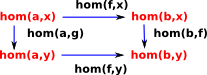We require this hom functor to interact nicely with the hom sets so the diagram on the left needs to commute.

This gives rise to a bi-functor to the category of sets:

C^op×C->Set

A bifunctor is a functor in two arguments, it could be written H(C^op,C)->Set . That is, it is contravarient in the first argument and covarient in the second).

Next steps

Hom sets are used in the page about the Yonada Lemma to relate structures at different levels of abstraction.

Other Related Pages

• Hom sets can be objects of a category which is the exponential object discussed on page here.
• The page here discuses homsets from a set theory perspective.
• Other related pages are:
  • functors
  • arrows

EuclideanSpace

home

Related Pages

• Hom sets can be objects of a category which is the exponential object discussed on page here.
• Hom sets are used in the page about the Yonada Lemma to relate structures at different levels of abstraction.
• The page here discuses homsets from a set theory perspective.
• Other related pages are:
  • functors
  • arrows