On these pages we discuss higher order categories.
We take first order category theory as consisting of objects and arrows between them.
There are various ways we can think about second order categories:
- By the addition of arrows between arrows (with appropriate axioms, these second level arrows are natural transformations).
- By allowing us to 'look inside' one layer of objects.
We can then go on to higher order objects by continuing the process (such as arrows between arrows between arrows and so on).
| order | between arrows | inside objects (in terms of components in D) |
|---|---|---|
| 1st order |  |
|
| 2ndorder |  |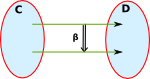
 |
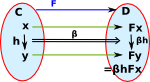| higher order | ||
This is often described in terms of n-cells. In the diagrams below, the number of lines (Shafts) in the arrows indicates the order of the arrow.
| 0-cell | 1-cell | 2-cell | 3-cell |
|---|---|---|---|
| object | arrow | arrow between arrows | arrow between arrows between arrows |
 |
 |
 |
 |
Quasi-Category
A quasi-category is a generalisation of the notion of a category. In a category the composition of two morphisms is uniquely defined but in a quasi-category all the morphisms that can serve as composition of two given morphisms are related to each other by higher order invertible morphisms.
Definition of Quasi-Category as a Simplicial SetA quasi-category is a simplicial set A in which every inner horn can be extended (not necessarily uniquely) to a simplex. That is, for every map /\k[n] -> A (0<k<n), there exists an extension Δ[n] -> A along the inclusion /\k[n] ->Δ[n]. |
 |
Where:
|
Example of a 2-dimensional simplex. |
Example of a 2-dimensional horn with face opposite 0 missing. |
More about:
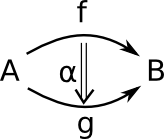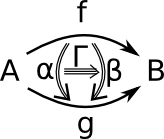Multicategories
Another way to represent higher order categories is multicategories. In this case the arrows can have multiple inputs. |
 |
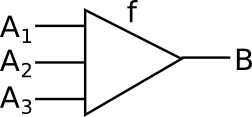Further topics
On the following pages we discuss some concepts of category theory, such as,
 |
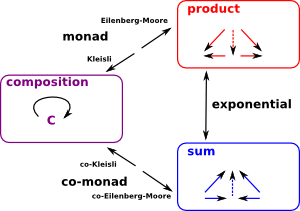
Natural Transformations |
 |
Monads |
 |
f-algebra |
 |
f-coalgebra |
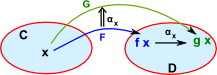
A given category 'C' with an endofunctor gives rise to a monad. By reversing the arrows (changing C to Cop) we can change the monad into a co-monad. It may be that monad and co-monad occur together. This happend when 3 adjoint functors are composed: L Examples:
|
 |
UEnriched Category
A category in which the hom-sets carry some extra structure, and that structure is preseved by function composition.
