Abstraction
One of the most important approaches is abstraction. In mathematics we may look at specific structures and then 'abstract' away the details to get to more general results.
For example, if we discover a structure, we try to discover the laws which govern it (usually in the form of equations - identities or axioms). We can then consider these laws on their own and work out the most general structures which satisfy them.
Structures
This section contains maths topics which involve abstract concepts and discrete (non continuous) mathematics.
- Sets
- Logic
- Boolean Algebra
- Graph Theory
- Category Theory
- Combinatorics

Terminology
- Field - Commutative division ring (different meaning of the word 'field' than fields on a manifold)
- Integral Domain - Commutative Ring with unity and no zero divisors
- Vector Space - Vectors over a field, Addition with scalar multiplication (vector & field (scalars))
- a(v+u) = a v + a u
- (a + b) v = a v + b v
- a (b v) = (a b) v
- 1 v = v
- Zero Divisor - A non-zero element 'a' of a commutative ring 'R' such that there is a non-zero element b
 R with ab=0
R with ab=0
Foundational Mathematics
Certain theories (set theory, type theory, category theory, logic/proof theory, etc.) appear to have the potential to provide an underpinning for the rest of mathematics.
Set Theory
A set can be thought of as a collection of elements where there are no duplicates and order is not significant.
| set |
So in set theory we can ask the question: 'is a given element a member of the set ?' |
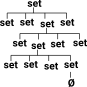 |
When fomalising set theory we can consider everything to be a set, so the elements are also sets. So its sets all the way down, until we get to an empty set (although a set can't contain two empty sets). Or perhaps it never ends (see 'open set'). |
Type theory
A type can also be thought of as a collection of elements but the elements are defined only for a given type and don't exist outside it. So, for example, the same element can't be a element of two different types.
Elements of a type can optionally be types themselves but, as with sets, a type must not contain itself. That is, it must be a strict hierarchy (no loops). See type universes.
Category Theory
In category theory we are mostly concerned with the external structure, that is, the properties of functions between objects (arrows). For instance: do diagrams of arrows commute (often upto isomorphism).
