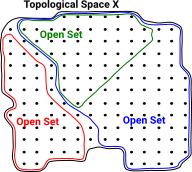
Open and closed sets give us a way to define concepts such as nearness and connectedness without needing a metric space.
Finite Open Sets
Here we denote the open sets with a finite set of symbols.
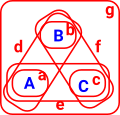 |
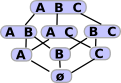
Example - discrete topologyØ = {} |
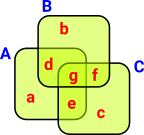
In this example there are 3 open sets denoted by the blue letters A, B and C. We define these open sets by elements they contain, here denoted by the red letters a, b, c, d, e, f and g. A := {a,d,e,g} |
 |
Poincaré duality
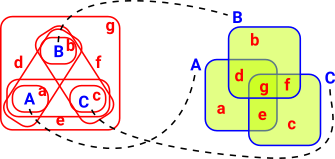 |
On the left of this diagram the blue letters A, B and C represent points, on the right the blue letters represent sets. The lower case red letters a, b, c, d, e, f and g are sets on the left and points on the right. |
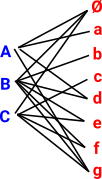 |
| Here we take 3 spaces A,B and C. Then we generate all possible unions and intersections. | 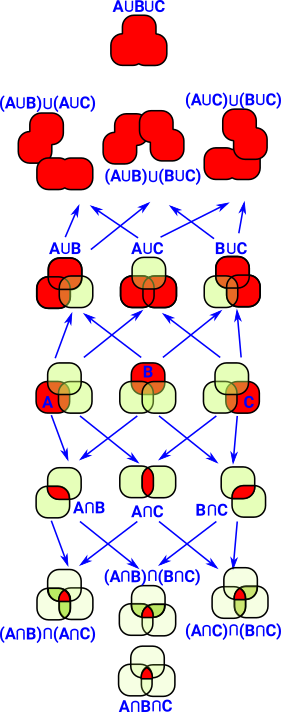 |
Topology on a Set
A topology on a set X is a collection τ (tau) of subsets of![]() (X), called open sets satisfying the following properties:
(X), called open sets satisfying the following properties:
- X and Ø are elements of τ.
- τ is closed under finite intersections.
- τ is closed under arbitary unions.
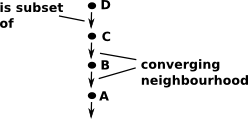
Neighborhood
A neighborhood of x is any open set U containing x.
We want to encode concepts like nearness, convergence and continuity. To do this we use the concept of neighborhood. We think of a 'space' as a set of points.
 |
How do we map from a set of points to neighborhood? An arbitrary mapping would not necessarily have properties like nearness. |
| We can look at the reverse direction: given a neighborhood 'Τ' how do we specify a point. |  |
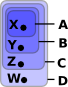 |
We can keep taking subsets that converge on a point. So we don't have a numerical measure of nearness but we know the points in set 'A' (such as 'X') tend to be closer to each other than, say, the points in set 'B' and so on. |
| We can define morphisms between these neighborhoods (open sets). So, for instance, 'A' can map to 'A' but it can also map to 'B' because all points that are in 'A' are also in 'B'. However 'B' cannot map to 'A' because there may be some points that are in 'B' but are not in 'A'. | 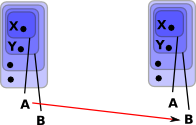 |
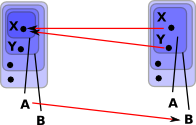 |
In order to make this diagram commute we need to be able to map the individual points. However 'X' on the left needs to map to both 'X' and 'Y' on the right and a function can't do this. The only way that we can do that is to reverse the direction of the arrows. So a morphism of open sets is 'contravarient', that is, it goes in the opposite direction to the mapping of the points. |
 |
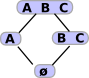
These subsets can be drawn like this. More generally (semi)lattice. |
Open Set Definition
The open sets of X need to satisfy the following:
- X and Ø are open sets.
- If U, V are open sets then U
 V is open.
V is open. - If ( Uλ)λ
 Lis any family of open sets then
Lis any family of open sets then λ
λ L Uλis open.
L Uλis open.
So different topologies can be defined by specifying the (semi) lattice structure:
 |
Discrete topology |
 |
|
| Trivial topology |
Examples
Metric Space
Infinite Sequences
Polynomials in n Variables
Zariski topology
Well-ordered Set
Every well-ordered set can be made into a topological space by endowing it with the order topology.
see Wikipedia
Upper Closure (upward closed set )
If, for every open set, we include the open set of all its unions and intersections and then include the unions and intersections of these and so on (closure) we would have every element of a connected topology in every neighborhood. To avoid this we only apply closure in one direction (up or down).
Subset Structure of Open Sets as Category
Subsets give interesting structure to open sets. This allows us to define a category of topological spaces. We can also further elaborate this subset structure to get fibre bundles and sheaves.
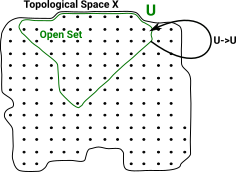
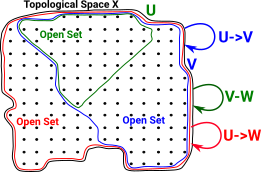
In this diagram the open set U is a subset of V. U We can represent this as an arrow from V to U V->U |
 |
This has the properties we expect from a category, for instance, the identity map: U->U (identity map) |
 |
and composition (U->V)*(V ->W) = U->W (composition) |
 |
Subsets of the Poweset
This diagram shows in more detail how we can take subsets of the Powerset and that this is contravarient. On the top-left is a set consisting of elements A, B and C. We map this into a two-element set below it containing 'AB' and C. We can think of this joining of A and B as indicating that the two points are connected. |
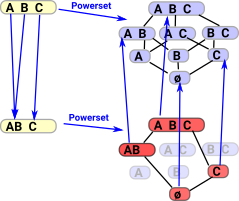 |
If points 'A' and 'B' are connected in 'X' then if an element of corresponding powerset contains one of them then it must contain both. In other words subsets which contain only 'A' or only 'B' are excluded.
Open Set Criterion for Continuity
A map ƒ: M1 -> M2 is continuous if and only if the inverse image of every open set is open.
