An isomorphism between two mathematical objects is a comparison between the two objects similar to equality. However an isomorphism is weaker and more general.
- Two objects are equal if they are exactly the same in every respect.
- Two objects are isomorphic if they have exactly the same mathematical properties.
For sets and mathematical structures based on sets we can define isomorphism using mappings in the following precise way:
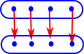
| Given two mathematical objects 'C' and 'D' that we want to compare, we construct two morphisms between them 'F' and 'G' as shown in this diagram: | |
| 'F' and 'G' must be chosen such that, by applying them one after the other (composing them), we get back exactly where we started, That is: | |
| GF = 1C | |
| FG = 1D |
If we can do this then the objects 'C' and 'D' are isomorphic to each other.
Isomorphism is weaker than equality but it is defined using equality of mappings. That is, by using equality of mappings we can only compare the objects 'upto isomorphism'.
Isomorphism for Sets
In the case of sets this means that C & D have the same number of elements and that there is a 1:1 mapping between them.
Alternative definition for maps between sets: A map f is called an isomorphism if there exists another map f-1 which is both a retraction and a section for f.
An automorphism in the category of sets is called a permutation.
Isomorphism for Groups
Lets take an example of groups, the first group has a binary operation '*' and the second group has a binary operation 'o'.
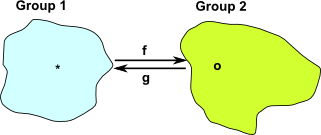
For an isomorphism to exist there must be a function 'f' from group 1 to group 2 such that:
f(x) o f(y) = f(x * y)
For an isomorphism to exist there must also be an inverse function 'g' from group 2 to to group 1.
g(x) * g(y) = g(x o y)
We can take this to a higher level of abstraction using category theory:

Now 'F' is a functor between category C and D and 'G' is a functor in the reverse direction. For this to represent an isomorphism then 1 = GF and FG = 1