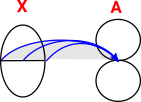
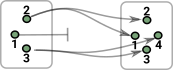
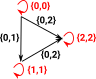Simplicial sets are similar to delta complexes (it may help to get an intuitive understanding to look at delta complex page first).
Simplicial sets have some nicer mathematical properties. If we think of delta complexes as being defined in terms of a set (or setop), with certain maps, then we can think of simplicial sets in terms of order preserving maps. We can use them as combinatorial models for the (weak) homotopy type of topological spaces with continuous maps between them (see ncatlab website).
 |
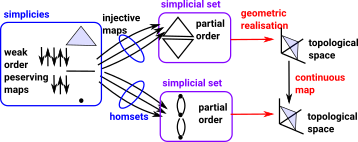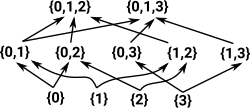
This diagram is intended to be an overview of the various types of maps involved. There is a lot going on in this diagram so I will attempt to explain the parts separately below. |
Maps in SetWhat really determines how categories such as set, setop and Δ work are their morphisms. Functions on set can be decomposed into surjective functions and injective functions. |
 surjective function |
 injective function |
|
Maps in SetopThe face and degeneracy maps are not functions, we are not in the category of set. A total function in set must give an element in the codomain for every element in the domain, face and degeneracy maps don't do that. They are valid arrows in category theory, but in Δ not set. These are more similar to the arrows in setop although, in addition, they must be order preserving: |
face map |
degenerate map |
Face Maps and Degeneracy Maps
Face Map
|
 |
Degeneracy Map
|
 |
Fibrations and Continuous Maps
Some continuous maps between spaces have a 1:1 mapping between points, these continuous maps are known as homeomorphisms. It is also possible to have a continuous map from a line to a point, or vise versa, that is what we are discussing here.
 |
There is a continuous map from a line to a point. In the same way that in sets, attempting to reverse a surjective map leads to fibre bundles, with continous maps we get fibrations. |
 |
This continuous map is reversible so we have a continuous map from a point to a line. |
| So, for example, two circles that touch at a point can be continuously deformed into a circle with a line through the middle. |  |
Or we can expand all the points on, say a circle, to get a band. This is like a product of a circle and a line. |
 |
For more information see:
Coding Fibrations as Simplicial Sets
So how can we model fibrations like this using simplicial sets? Lets look again at the example where two circles that touch at a point can be continuously deformed into a circle with a line through the middle.
Here is an attempt to code as a simplicial set. The deformation into a circle with a line through the middle is done by a degenerate map which creates two instances of point b. Note: the two degenerate points b must always have maps between each other. |
 |
As Continuous Map
 |
Here we are looking for a continuous map to map a topological space to map to something homotopy equivalent. As explained on page here a function f : X->Y is continuous if f-1(V) is open for every open set V in Y. Can we treat simplcies like open sets? So the simplcies map in the opposite direction to vertices? The simplcies may map to simplcies of a different dimension, so here the middle vertex maps to a bar (edge). This continuous map should preserve loops, does this do that? can we prove it? |
At Higher Level
 |
What rules follow from having degenerate points in the simplicial set? For example from this diagram here: |
| We can join the two b points on the left and fill in the triangle of b's. |  |
For more information see these pages:
Coding These Structures
The points are given a weak order, this gives a direction to faces. So if X is a point in a face then the next point Y is greater or equal to X. Mappings, such as face maps, are (weak) order preserving continuous maps.
If points have the same numeric value then they must be contractible to a single point.
Coding Simplex
Within a simplex we have a (weak) order. That is, for any 2 points x any y we have either x <= y or y <= x or both but not neither.
Coding Simplicial Set
Within a wider simplicial set consisting of simplicies glued together we have a (weak) partial order. So, in this case, some pairs of points may not be related in this way. That is, for any 2 points x any y we have either x <= y or y <= x or both or neither.
Simplicial Set as a Presheaf
The structure of simplicial sets and delta sets comes from two things:
- A sort of internal structure, for instance: an edge connects two vertices and a triangle has 3 lines on its boundary.
- A sort of external structure which allows us to build up complex shapes by gluing together common faces.
An alternative way to think of this is as local structure and global structure. This hints that this might be a presheaf.
(see sheaf page here)
We denote the simplicial set as:
X: Δop -> Set
where:
- Δ is a finite totally ordered set {0,1,2...,n} where the morphisms are order preserving. These are face maps and degeneracy maps as described below.
So I think we can think of these maps into set as a homset picking out each point, edge, triangle ... in the set.
Simplicial Sets and Category Theory
Simplicial sets are used to define quasi-categories, a basic notion of higher category theory.
Quasi-Category
A quasi-category is a generalisation of the notion of a category. In a category the composition of two morphisms is uniquely defined but in a quasi-category all the morphisms that can serve as composition of two given morphisms are related to each other by higher order invertible morphisms.
Definition of Quasi-Category as a Simplicial SetA quasi-category is a simplicial set A in which every inner horn can be extended (not necessarily uniquely) to a simplex. That is, for every map /\k[n] -> A (0<k<n), there exists an extension Δ[n] -> A along the inclusion /\k[n] ->Δ[n]. |
 |
Where:
|
Example of a 2-dimensional simplex. |
Example of a 2-dimensional horn with face opposite 0 missing. |
More about:
Geometric Realisation
As discussed in the introduction to this page we want to use simplicial set as combinatorial models for the (weak) homotopy type of topological spaces.
To model spaces as topological spaces we use a vector space where each point in the simplex has a seperate dimension. The higher order faces also have a vector space with a dimension for each face.
The simplicial set can then be defined by the maps between these vector spaces. These maps are linear (modeled by a matrix) which makes it easier to work with all these dimensions.
Topological Space and Simplicial Sets (Geometric Realisation)
Topological spaces have some nice properties, they have the concept of nearness in the most general way. However topological spaces have some quite stringent requirements, geometric realisation gives use a way to embed any CW complexes or simplicial set as a topological space.
A first thought for how to embed simplicial sets in topological spaces might be to equate each simplex with an open set, unfortunately this won't work for the following reasons: |
 |
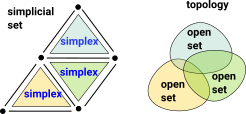- Every union of simplices in a CW complex is not a simplex but unions of open sets must be open sets.
- Every pair of simplices don't necessarily have an intersection.
There is a way to canonically get a topological space from a simplicial complex, this requires a much higher dimensional space so its not very intuitive. For instance, to encode a graph (2D complex), each vertex in the graph needs to have its own dimension in the topological space.
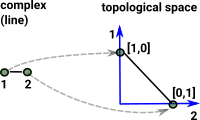
Here we want to encode a complex with two points and a line. We embed this in 2 dimensional Euclidean space (and therefore topological space).
Each of the points is now a vector in its own dimension, these are [1,0] and [0,1] and they are the basis vectors. The line is a straight line between these basis vectors, parameterised by t like this { (1-t)*[1,0]+t*[0,1] | t |
 |
 |
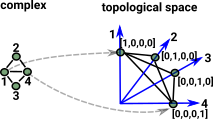A more complex graph gives a lot more dimensions which makes visualising the topological space harder. |
For more information about geometric realisation see the page here.
Simplicial Set from Delta Complex
To show Geometric Realisation, as a reminder from the delta set page, here is an example:
|
 |
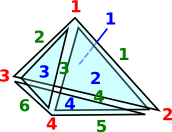| This representation holds all these indexes so that we don't have to keep creating them and they can be used consistently. | |
Face MapsSo the tetrahedron indexes its 4 triangles, each triangle indexes its 3 edges and each edge indexes its 2 vertices. Each face table therefore indexes into the next. To show this I have drawn some of the arrows (I could not draw all the arrows as that would have made the diagram too messy). |
 |
 |
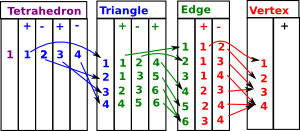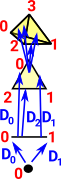The delta category Δ has:
The vertices of the simplicies are ordered by labeling them with natural numbers. Notation: [M] stands for a simplex with vertices 0 to M. For example: A morphism [M]->[N] is only defined if M <= N |
|
 |
Δop has the same objects as Δ but the morphisms are reversed. The morphisms are now the face maps and degeneracy maps. |
 |
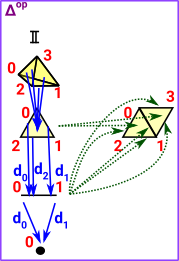We can then make this into a sheaf Δop->set (as described on page here). This separates out the structure inherent in the maps between simplicies of different dimensions and the structure which comes from gluing them together. Perhaps we can think of the simplex structure as the local structure and the gluing provides the global structure.
Gluing
We have a contravarient functor which picks out faces but the faces are not all separate so how do we encode this additional structure?
The edges are connected when they share a common sub-face.
 |
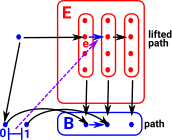In order to understand this we need the concepts of fibration and lifting as described on the page here. |
Paths
What happens when there are a sequence of edges following each other? (the target of the first is equal to the source of the second and so on). Can the edge in the interval Is this the same thing as requiring composition? In cubical type theory equalities are represented by a path, in a given space, between equal terms. |
 |
match the whole path? |
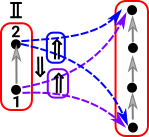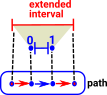In order to understand this we need the concepts of cofibration and extensions as described on the page here. |
Computing with Simplicial Sets
How should we construct simplicial sets in computer programs?
 |
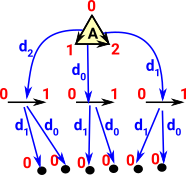SimplexStart with a simplex with no degenerate faces. |
| This can be viewed as a lattice. |  |
 |
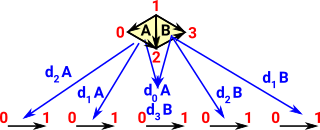ComplexThis time there are multiple faces at the top level glued together by having common faces. |
 |
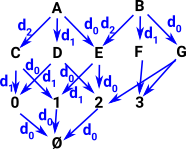Model Theory and Fibrations
See:
- Model Theory
- As (discrete) fibration (see page here also ncatlib)
- Kan fibrations
Simplicial Set as Presheaf
A simplicial set is a presheaf, that is, a functor from Δop to Set. This functor is a homset, we can think of it as picking out all the Δop shaped elements of the set. So it picks out the simplicies and gives them a local order. |
X: Δop -> Set where:
|
So how are connections between different faces recorded?
One way is as generator+relations, for example, if we have two triangles 'a' and 'b' and we want to join the diagonal (that is, join the (0,2) faces) we could do this with this relation:
d(a,1) = d(b,1)
where:
d is a face map (explained below) which gives a sub face when we remove vertex 1.
In category theory terms we can describe this in terms of morphisms between the functors described above. That is a natural transformation.
A simplicial set is a functor from deltaop to set. Where delta is a (weakly) ordered set as described on the page here. |
 |
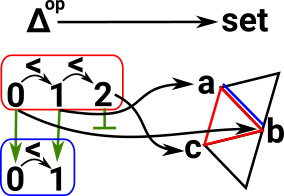When denoting faces in a complex, order is important for finding things like boundaries.
Simplicial sets are an extension to simplicial complexes (see page here).
To get to simplicial sets from simplicial complexes it is necessary to order (or partially order) the vertices.
In addition to the face maps in simplicial complexes we add degeneracy maps in the opposite direction these maps are order preserving.
Simplicial sets have an additional property that they are closed under products and this is important in Cubical TT for example.
Degeneracy
In homology (as described on the page here) the emphasis is on the relationship between adjacent dimensions. For instance, if we take the boundary, we map from a given dimension to the dimension immediately below it (face maps). This situation can be modeled by simplicial complexes already described on the page here.
In homotopy (as described on the page here) we may have an n-dimensional path in a dimension several levels higher. This situation may be better modeled by simplicial sets as described here.
| For a 2-dimensional face in 2-dimensional space all the vertices have different indices. |  |
For a 0-dimensional point in 2-dimensional space we can use the same index multiple times. This is an example of a degenerate face. |
 |
Combinatorics
Why Ordered Structure?
The ordering of vertices (0-simplicies) gives a direction to edges (1-simplicies) thought of here as functions or mappings. Although the mappings have a positive direction they may be reversible. It also allows a 2-simplex to represent the composition of two mappings/edges. On the diagram on the right the edge {0,2} is the composition of {0,1} and {1,2}. So the diagram shows all possible ways to get from vertex-0 to vertex-2. |
 |
 |
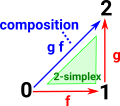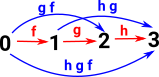This can be extended to 3-simplicies. Here f, g and h are mappings where g can be applied after f and h can be applied after g . So the 3-simplex represents all possible ways these 3 functions can be composed in series while retaining that order. So the diagram shows all 4 possible ways to get from vertex-0 to vertex-3. |
 |
So, in general, an n-simplex gives us all the possible ways to get from the smallest to the largest numbered vertex. This gives us all the compositions of the maps.
In some ways the maps f, g and h seem like 'generators' where we can generate the other sub-faces, from these, by composition. So we start off with something that is linear and we get a 'solid' simplex.
The face and degeneracy maps are order preserving maps between these structures.
Face MapsHere a face map does not map vertex 1 so we get the composition without its component parts. |
 |
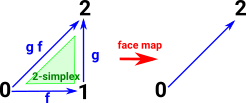Degeneracy MapsAbove, when we were looking at all possible routes from vertex-0 to vertex-1 there are additional possibilities, we could have inserted self loops (identity functions) at any of the nodes. We now have an infinite number of routes since we can go round these loops any number of times. A degeneracy map inserts a loop at a given node. |
 |
x
The degeneracy loosens the coupling between dimension and number of elements.
The following table shows the possibilities in a combinatorial way.
Each entry must be ordered, the element values can stay the same (degeneracy) but they must not decrease.
Degenerate entries (where an element occurs more than once) are shown in red.
| n | Δ0 | Δ1 | Δ2 | ... | ||||
|---|---|---|---|---|---|---|---|---|
| 0 | {0} | {0} {1} |
{0} {1} {2} |
|||||
| 1 | {0,0} |
|
|
|||||
| 2 | {0,0,0} | {0,0,0} {0,0,1} {0,1,1} {1,1,1} |
{0,0,0} {0,0,1} {0,0,2} {0,1,1} {0,1,2} {0,2,2} {1,1,1} {1,1,2} {1,2,2} {2,2,2} |
|||||
| 3 | {0,0,0,0} | {0,0,0,0} {0,0,0,1} {0,0,1,1} {0,1,1,1} {0,1,1,1} |
{0,0,0,0} {0,0,0,1} {0,0,0,2} {0,0,1,1} {0,0,1,2} {0,0,2,2} {0,1,1,1} {0,1,1,2} {0,1,2,2} {0,2,2,2} {1,1,1,1} {1,1,1,2} {1,1,2,2} {1,2,2,2} {2,2,2,2} |
|||||
| ... |
Products
One of the advantages of simplicial sets, over simplicial complexes, is that they simplify products (products of simplicial complexes on page here). We can calculate products of simplicial complexes but it requires arbitrary choices about which points to choose. Because a simplicial set is ordered no choices are required, the product is unique.
In a simplicial set the concatenation of two simplicies is a simplex but the product of two simplicies is complex.
| concatenation of 2 simplicies | product of 2 simplicies | |
| simplicial set | simple |
complex |
cubical set A cubical version of simplicial sets is described on the page here. |
complex |
simple |
Example 1 - Product of 2 lines Δ1×Δ1
Here is a simple example, the product of 2 edges, we would expect this to give a square.
The simplicies are total orders so we are trying to find all the total orders in the simplicial set.
 |
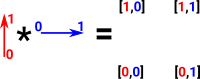The Cartesian product of the points is 4 points denoted by a pair [a,b] giving all possible combinations of the endpoints of the edges. So the points of this product are:
|
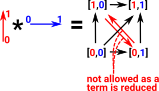
The cartesian product of the edges is given by all possible routes (total orders) between [0,0] and [1,1]. This is subject to the condition that, for the route to be included, then both the numeric values in the point must increase or, at least, stay the same. So, for example, there is no route between [0,1] and [1,0] because one number goes up and the other goes down so we cant go in either direction between them. |
 |
Where the paths enclose a triangle then we include that. |
 |
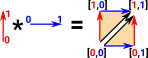More General Method
The method described above still relies on a certain amount of geometric intuition, it is possible to have a more combinatoric algorithm that is simpler to compute.
This makes use of the ability to have degenerate faces.
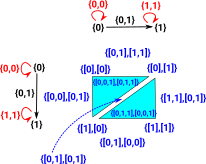
Example 1 Continued - product of 2 lines Δ1×Δ1Multiplying out all the terms at each dimension and canceling out duplicates as above gives: points:
edges - there are 5 edges where neither dimension goes down:
triangles:
|
 |
Products of Simplicial Sets
For K,L (K×L)k=Kk×Lk and whose face- and degeneracy maps are, similarly, the image under the Cartesian product-functor of the face and degeneracy maps of the factors. |
 |
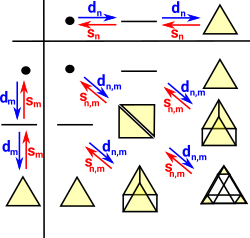Since SimplicialSets is a category of presheaves, namely over the simplex category, this is a special case of the general fact that limits(such as products, pullbacks and inverse limits) of presheaves are computed objectwise. https://ncatlab.org/nlab/show/limits+of+presheaves+are+computed+objectwise
So an element in product might be (a,b) and another element might be (c,d) then the product is:
(a,b) * (c,d) = (a*c,b*d)
For functions if we are mapping (a,b) to (f(a),g(b)) then the function between them is (f,g) which is two functions in parallel. So this can be drawn like this
(a,b) ---- (f,g). ---> (f(a),g(b))
This can be decomposed like this
(a,b) ---- (f,id). ---> (f(a),b) ---- (id,g). ---> (f(a),g(b))
or like this
(a,b) ---- (id,g) ---> (a,g(b)) ---- (f,id). ---> (f(a),g(b))
These 3 paths give 2 triangles which is what we would expect from geometric intuition of the product of two lines.
The rules are:
- (X × Y)n = Xn × Yn = {(x,y) x
Xn, yYn} - if (x,y)(X × Y)n then di(x,y) = (di x, di y)
- if (x,y)(X × Y)n then si(x,y) = (si x, si y)
To take the product of two simplicial sets multiply all the terms which have the same dimension. Duplicates can be removed, also degenerate versions of existing terms can be removed, for example:
{[0,0],[1,1]} = {[s0(0),s0(1)]} = s0{[0],[1]}
so that can cancel out with {[0],[1]}
Skeleton The product is given by all possible paths (chains) where one of the multiplicands is changed at a time (we can think of the other as being the identity (Id) function). On the diagram we can think of this as using the vertical and horizontal lines.
|
 |
||
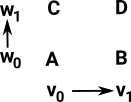Nerve Shuffling Operation Shuffles are partitions of the set {0,1,...,m+n} into two disjoint subsets.
|
where:
|
This works out automatically if we work in terms of edges by coding vertices as degenerate edges as follows:
line1 ={v0->v1,v0->v0,v1->v1}
and we want to multiply this by another line:
line2 ={w0->w1,w0->w0,w1->w1}
so by multiplying out all the terms we get line 1 * line 2 =
(v0->v1)*(w0->w1) = (v0,w0)->(v1,w1) = A->D
(v0->v1)*(w0->w0) = (v0,w0)->(v1,w0) = A->B
(v0->v1)*(w1->w1) = (v0,w1)->(v1,w1) = C->D
(v0->v0)*(w0->w1) = (v0,w0)->(v0,w1) = A->C
(v0->v0)*(w0->w0) = (v0,w0)->(v0,w0) = A->A
(v0->v0)*(w1->w1) = (v0,w1)->(v0,w1) = C->C
(v1->v1)*(w0->w1) = (v1,w0)->(v1,w1) = B->D
(v1->v1)*(w0->w0) = (v1,w0)->(v1,w0) = B->B
(v1->v1)*(w1->w1) = (v1,w1)->(v1,w1) = D->D
This gives 9 edges of which 4 are degenerate (vertices). The non-degenerate edges form the boundary of two triangles. |
 |
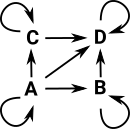Example2 - product of triangle and line
|
 |
||
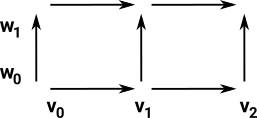Nerve Shuffling Operation Shuffles are partitions of the set {0,1,...,m+n} into two disjoint subsets.
|
where:
|
This works out automatically if we work in terms of edges by coding vertices as degenerate edges as above.
Simplicial Sets and Topology
Simplicial sets are not directly mappable onto topological spaces, that is simplicies do not direcly correspond to open sets. We can convert between simplicial sets and topological spaces but its more complicated than that and we have to go via linear algebra.
Continuous Maps
In the same way that, in set theory, maps can be decomposed into surjective and injective maps, in topology/homotopy continuous maps can be decomposed into face maps and degenerate maps (Right Lifting Property - RLP and Left Lifting Property - LLP).
Simplicial Set as Fibration
| A fibration has the lifting property so simplex structures are lifted into complex structures. |  |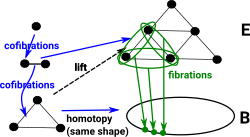
The degenerate faces then come from the homotopy extension property (HEP) see page here.
Modeling Simplicial Sets Using Order Preserving Maps
We need to work with continuous maps between topological spaces, these continuous maps are defined as follows:
| Let X and Y be topological spaces. A function f : X->Y is continuous if f-1(V) is open for every open set V in Y. |  |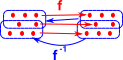
How are continuous maps related to order preserving maps?
see Wiki
Example of Homotopy Extension Property (HEP)
| Imagine we have a space represented like this: |  |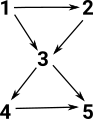
Is it homotopy equivalent to this space? What are the numbers of the nodes? |
 |
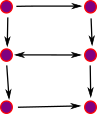Start with the numbers above but split '3' using the homotopy extension property (see the page here). This works provided that '3' is contractible (there is a retraction to the terminal object). This means that there must be an arrow in each direction between these degenerate 3's. So it doesn't matter which of them the other arrows go in or out of, allowing us to draw it like this: |
 |
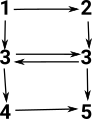Why might Simplicial Set be related to Proofs?
In set, given a total function, every element in the domain determines an element in the codomain.
In setop it is the other way round, every element in the codomain determines an element in the domain.
In reverse proofs, that is we start with what we want to prove and work back to the reasons why it is true, we need something more like the second case.
Of course forgetting and duplication information is not enough, on its own, for a proof. We also need, say, deconstructors from type theory.
In cubical type theory degeneracy maps corresponds to weakening in Logic.
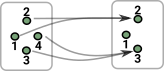
Example Graph
 |
This is a simplicial set with only vertices and edges. |
The category theoretic approach is to investigate objects, in this case graphs, in terms of the arrows (morphisms) between objects. So we are probing it from the outside.
The internal view can be more intuitive, especially to newcomers to category theory, so here we are relating the internal and external views to help with intuition. A graph is similar to a category theory diagram, but is weaker, in the sense that there is no requirement for compositions and identity loops to exist. Although category theory diagrams and graphs are different in this way here we see how they interact so we can get some information about the graph from its category theory diagram.
To do this we need to work with all the arrows from an object so we need to have the concept of a homset (see page here)
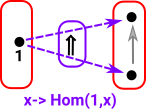
As a start with this approach we want to probe the red object on the right: To do this start by 'probing' it with arrows from a graph with only one vertex and no edges. All the possible arrows from the single vertex object form a homset. This homset is a set (where the elements are arrows) so we can use our set theoretic intuition on it. This set has one object for every vertex in the object. |
 |
 |
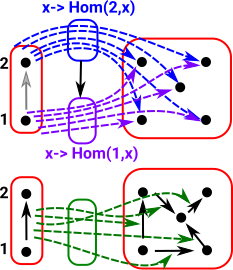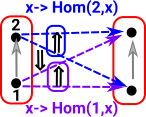
Now we need to 'probe' the edges. We can do this with an arrow from a graph with a single edge between two vertices. The bottom part of the graph on the left shows arrows (green) to each edge. So this time we have a homset which gives the number of edges. However, the mapping of the edges needs to play well with the mapping of the vertices (top part of diagram).
Similarly with vertex 2
|
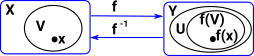
It is easier to see this contravarience from a simpler diagram. If 'F' is given we can derive 'h' from 'g' by composing with 'F' but we can't derive 'g' from 'h'. So if we want to get the usual functions in set we need to start with Grfop A contravarient functor of the form Cop->set occurs in other structures and is called a presheaf as described on page here. |
 |
 |
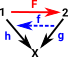This graph object that we are using to 'probe' another graph object is known as a representable object in Grf (see Yoneda lemma page). This representable object is a graph with two vertices and an arrow between them. |
- More about relating category theory to set theory view of graphs on page here.
- We can extend this example from graphs to simplicial sets as described on page here.
Example Triangle
 |
Things get more complicated when we move up from lines to surfaces. There are 3 ways to get from a triangle to an edge (by deleting each node) and 2 ways to get from a edge to a triangle (degenerate map from each end of the edge). |
A face, such as a triangle, contains its boundary, such as the edges and nodes. If we take all the permutations of 3 numbers in (non strict) order we have 1 for each node, 1 for the whole triangle but 2 for each edge. |
 |
| In addition to the mapping into the line (described on page here.) we now have mapping into a triangle. That is triangle is representable object. |  |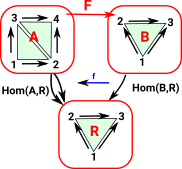
Putting it all Together
Here is an example consisting of two triangles. A simplicial set involves many mathematical structures such as sheaves. Attempting to show everything in one diagram gets very messy but I'll try. |
 |
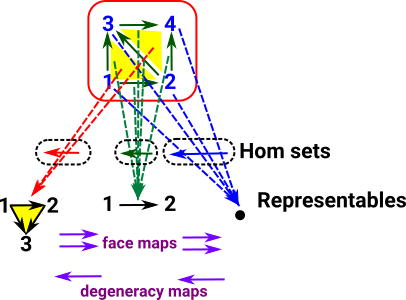If we treat vertices, lines, triangles ... as separate objects, with only face maps between them, then we have a similar situation to the delta complex structure (see page here). But this is not a single sheaf. It would be nice if we could combine the objects to have a single sheaf and combine all the hom sets. |
 |
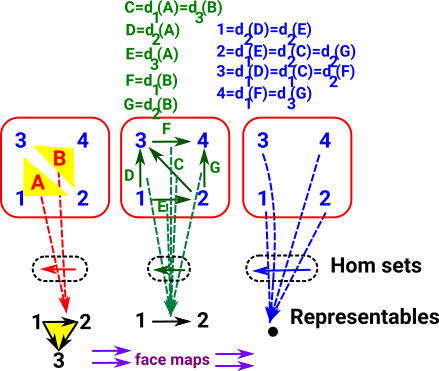So can we use degenerate versions of higher dimensional faces to represent lower dimensional faces? For example, if we are collapsing vertex 2 down to vertex 1 we might use: d2 s1 |
 |
But there doesn't seem to be a way to reverse this, that is, to take a degenerate object and split it out to two non-degenerate vertices. Can we use equations externally to add and remove this degeneracy? |
 |
Algebra of Simplicial Sets
We can represent simplicial sets as generators+relations.
Here we glue two faces of simplicies to form a simplicial set. So here we have glued (a0) to (b1) and (a1) to (b0) to form a loop. So if we apply M twice we get back to where we started. We can express this as a group presentation like this: [M | M*M=1] |
 |
In the next example there are 3 gluings (a0) to (b1) (b0) to (c1) (c0) to (a1) to form a loop. So if we apply R 3 times we get back to where we started. We can express this as a group presentation like this: [R | R*R*R=1] |
 |
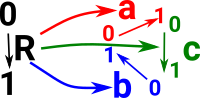| We can take the product of these two examples: |  |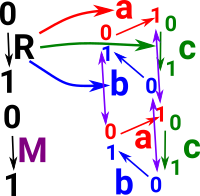
Gluing in 2 dimensions
So here we have glued (A1,A2) to (B2,B1). So, order is not preserved over the whole simplicial set, just over an individual simplex. The whole simplical set is not a total order as there are faces (for example A0 and B0) which cant be compared. We can glue any dimension face (point, line, triangle... ) as long as the two faces being glued have the same dimension. |
 |
We can then go on to glue more faces, for instance, in addition to gluing (A1,A2) to (B2,B1) as above we could additionally glue (A0,A1) to (B1,B2). Note that, in this case, this only leaves one remaining face. This is known as a horn clause, this means that the remaining face is also equal. I t also means that the two simplicies are also equal or opposite. |
 |
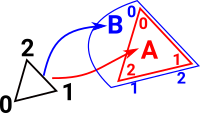| Or we can glue more simplicies. For instance we can glue (A0,A1) to (C1,C0) |  |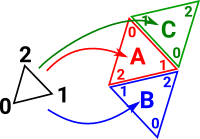
By doing this gluing we define an equivalence relation over the top of the original ordered set. To do this we can either construct the quotient space, that is S\~ where S is the original ordered set and ~ is the equivalence relation. This effectively makes them the same point (which may not work with the ordering) or we use a setoid to represent ~ over S. |
 |
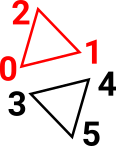see
Subset Structure
Above we have the set of all functions into the complex which is a homset. We can treat this homset as a set (see Yoneda) that is ignore the structure below it so that it is a set category including functions (the structure above it). A structure we can take from the homset is the subset structure. |
 |
Face Maps and Degeneracy Maps
A face map removes the nth vertex. In this case d1 removes vertex 1. |
|
| Any higher sub faces containing the removed vertex are also removed. |  |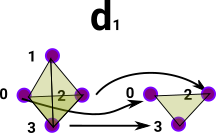
In order to handle the degenerate faces better we add degenerate maps going in the reverse direction to the face maps.
A degeneracy map duplicates the nth vertex. In this case s1 duplicates vertex 1. |
|
| Any higher sub faces are also duplicated. |  |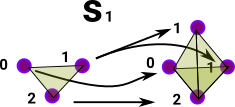
Structure like identity functor (reflexitivity) is duplicated and there are id functors between the degenerates. So if we have reflexitivity and transitivity then structure (such as lines) into one of the degenerates also goes into the other. But can we always assume reflexitivity and transitivity? |
 |
If the 'vertices' have internal structure is that duplicated? If we have permutations, is this a groupoid? |
 |
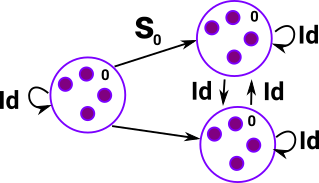Grading of Number of Dimensions
The maps going in both directions increment and decrement the number of dimensions: Face Maps di : Degeneracy Maps sj : Takes an n-simplex and gives its j-th degenerate (n+1) simplex inside it. |
 |
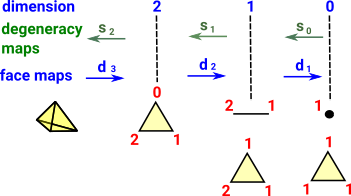Face Maps
di : Xn -> Xn-1 | 0≤i≤n
Degeneracy Maps
sj : Xn -> Xn+1 | 0≤j≤n
Simplicial Identities
The following is based on a category of ordered sets, Order preserving arrows can be decomposed into a sequence of arrows that insert or merge single elements one at a time. More about ordered sets on page here.
Note: when combining maps below the map on the right is done first. For example, di dj means do dj then do di.
| Identity | An example of one case in a triangle {0,1,2} |
|---|---|
| di dj = dj-1 di if i < j |  |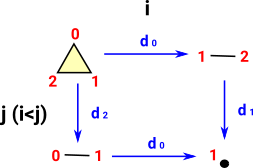
| di sj = s j-1 di if i < j |  |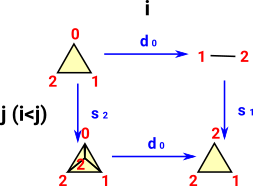
| dj sj = id = dj+1 sj |  |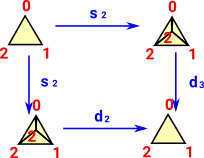
| di sj = sj di-1 if i > j+1 |  |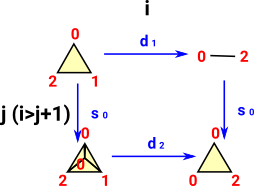
| si sj = s j+1 s i if i ≤ j |  |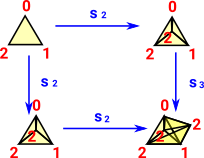
Skeleton
 |
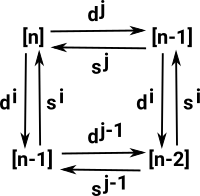Here are all the possible cases of the identities for the example of a triangle {0,1,2}.
example {0,1,2} |
|||||
| left hand side | right hand side | ||||
| 1st stage | result | 1st stage | result | ||
| di dj = dj-1 di if i < j | since i < j these are the only combinations allowed | dj | di dj | di | dj-1 di |
| i=0,j=1 | {0,2} | d0d1={2} | {1,2} | d0d0={2} | |
| i=0,j=2 | {0,1} | d0d2={1} | {1,2} | d1d0={1} | |
| i=1,j=2 | {0,1} | d1d2={0} | {0,2} | d1d1={0} | |
| 1st stage | result | 1st stage | result | ||
| di sj = s j-1 di if i < j | since i < j these are the only combinations allowed | sj | di sj | di | s j-1 di |
| i=0,j=1 | {0,1,1,2} | d0s1={1,1,2} | {1,2} | s0d0={1,1,2} | |
| i=0,j=2 | {0,1,2,2} | d0s2={1,2,2} | {1,2} | s1d0={1,2,2} | |
| i=1,j=2 | {0,1,2,2} | d1s2={0,2,2} | {0,2} | s1d1={0,2,2} | |
| 1st stage | result | 1st stage | result | ||
| dj sj = id = dj+1 sj | sj | dj sj | sj | dj+1 sj | |
| i=0 | {0,0,1,2} | {0,1,2} | {0,0,1,2} | {0,1,2} | |
| i=1 | {0,1,1,2} | {0,1,2} | {0,1,1,2} | {0,1,2} | |
| i=2 | {0,1,2,2} | {0,1,2} | {0,1,2,2} | {0,1,2} | |
| 1st stage | result | 1st stage | result | ||
| di sj = sj di-1 if i > j+1 | since i > j+1 these are the only combinations allowed | sj | di sj | di-1 | sj di-1 |
| i=2,j=0 | {0,0,1,2} | {0,0,2} | {0,2} | {0,0,2} | |
| 1st stage | result | 1st stage | result | ||
| si sj = s j+1 s i if i ≤ j | since i ≤ j these are the only combinations allowed | sj | si sj | s i | s j+1 s i |
| i=0,j=0 | {0,0,1,2} | {0,0,0,1,2} | {0,0,1,2} | {0,0,0,1,2} | |
| i=0,j=1 | {0,1,1,2} | {0,0,1,1,2} | {0,0,1,2} | {0,0,1,1,2} | |
| i=0,j=2 | {0,1,2,2} | {0,0,1,2,2} | {0,0,1,2} | {0,0,1,2,2} | |
| i=1,j=1 | {0,1,1,2} | {0,1,1,1,2} | {0,1,1,2} | {0,1,1,1,2} | |
| i=1,j=2 | {0,1,2,2} | {0,1,1,2,2} | {0,1,1,2} | {0,1,1,2,2} | |
| i=2,j=2 | {0,1,2,2} | {0,1,2,2,2} | {0,1,2,2} | {0,1,2,2,2} | |
Functor to Set
So how do face maps get transported from Δop to set? Vertex 1 needs to be removed from all faces. |
 |
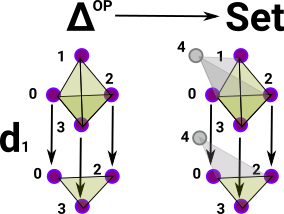| and how do degeneracy maps get transported from Cop to set? |  |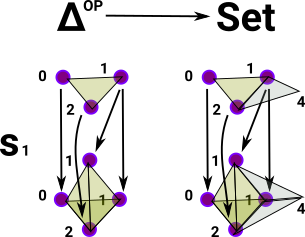
Model Category
| A model category is a context in which we can do homotopy theory or some generalization thereof; two model categories are ‘the same’ for this purpose if they are Quillen equivalent. (nlab) |  |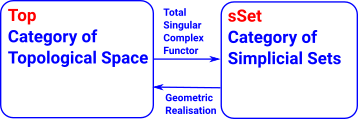
A model category (sometimes called a Quillen model category) is a context for doing homotopy theory.
It is a category equipped with three classes of morphisms, each closed under composition:
| related structure in set | |||
|---|---|---|---|
| weak equivalences | bijection | ||
| fibrations | nice surjections (Serre fibrations) | ||
| cofibrations | nice inclusions | neighborhood retract |
Model Category in CTT
We have some nice properties if mappings are continuous. The most general form of continuous map is mapping between topological spaces where all open sets in codomain have preimage which is an open set. However, lines are not open sets in general. To get these properties we need to restrict to structures where we do have these properties such as maps between simplicies.
Fibration in CTT
A fibration allows us to 'lift' a line between two points to a line between two structures. This is called the homotopy lifting property (HLP). In this diagram the blue lines show the mapping of points and the green line maps lines (like open set) in the opposite direction to the points. |
 |
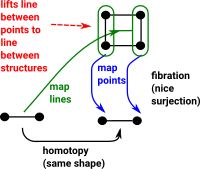Cofibration in CTT
A cofibration allows us to 'extend' a mapping from a subset to a mapping from the whole structure. This is called the homotopy extension property (HEP). Again the blue lines show the mapping of points and the green line maps lines (like open set) in the opposite direction to the points. |
 |
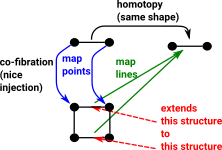Quillen Equivalence
We need a mapping that preserves the structure of a topological space: the cycles, the boundaries, the holes and so on. However it does not need to conserve the exact points, faces of the complexes that hold them. The two shapes on the right are the same from a topology point of view they are a disk with a boundary round it. |
 |
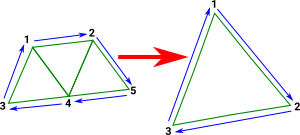| In order to do this we map the connections between the dimensions in the chain (boundaries), not the dimensions (points, faces, etc.) themselves. |  |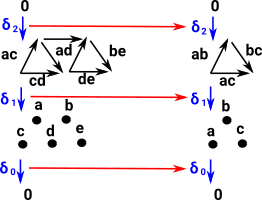
Simplicial Set in Category Theory
| Objects | Morphisms | |
|---|---|---|
| Δ | ordered sets example: {0,1,2} |
Order preserving maps may be inclusions (add points), example: {0,1,2} -> {0,1,2,3,4} |
| Δop | ordered sets | Order preserving maps example: {0,1,2,3,4} -> {0,1,2} may remove points (choose a face). |
Chain Homotopy
Weak Equivalences
Usually equivalences are defined in terms of two functors in opposite directions however a weaker notion of equivalence is defined in terms of a functor going in one direction only.
Fibrations
A Serre fibration arises when we reverse the functor defining the weak equivalence.
Cofibrations
In any model category:
- A fibration that is also a weak equivalence is called a trivial (or acyclic) fibration.
- A cofibration that is also a weak equivalence is called a trivial (or acyclic) cofibration.
Cubical Type Theory
Cubical type theory extends these concepts with the idea of an interval [0,1]. This is discussed further on the page here.
Code
Sage is mathematical software which implements simplicial sets, more about this on page here.
Some Papers that use Simplicial Sets
[1] Daniel Quillen, Rational homotopy theory, Ann. of Math. (2) 90 (1969), 205–295.
[2] A. K. Bousfield and D. M. Kan, Homotopy limits, completions and localizations, Lecture Notes in Mathematics, Vol. 304, Springer-Verlag, Berlin, 1972.
U. 
