This can provide functionality from a simple hinged door, to a lattice framework, to a human body (loosely connected set of bones)
The idea is to build a program that will allow us to build virtual devices that can be built from standard components like Meccano or Lego.
Types of Joint
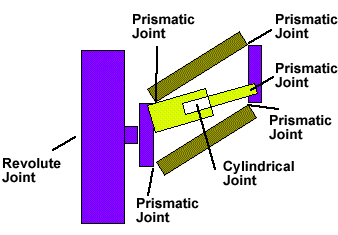
In the field of robotics (or cybernetics), six basic types of joint have been defined:
| Name | Symbol | DOF |
| Revolute joints | R | 1 |
| Prismatic joints | P | 1 |
| Helical joints | - | 1 |
| Cylindrical joints | RP | 2 |
| Spherical joints | 3R | 3 |
| Planar joints | RRP | 3 |
In character animation, only 2 types of joint need to be considered. These are the "revolute" and "prismatic" joints. All other types can be based on these two.
1 degree of freedom:
rotational joint - wheel.
hinge - similar to rotational joint above but with limits to motion (end stops)
2 degrees of freedom
ball & socket joint
Mathmatics of joints in dynamics systems
Joints might be thought of as a set of constraints on the dynamics equations describing the individual masses which are joined.
These constraints can be represented by equations.
One analytical solution would be to substitute the constraint equation into the dynamics equations. However this can lead to some complicated equations.
Another method to get a solution could be to use the method of Lagrange Multipliers.
Alternativly numerical methods could be used to solve the dynamics equations, with the constraints vetoing any movements not allowed by the joint.
Solving for the motion of masses connected by a hinge using Lagrange Multipliers
Lagrange Multipliers are explained on this page.Assume two masses, A and B, connected with a hinge. The only external forces acting on the system are:
- Fa = external force acting on the centre of mass of mass A.
- Fb = external force acting on the centre of mass of mass B.
And two torques acting on the system:
- Ta = external torque acting around the centre of mass of mass A.
- Tb = external torque acting around the centre of mass of mass B.
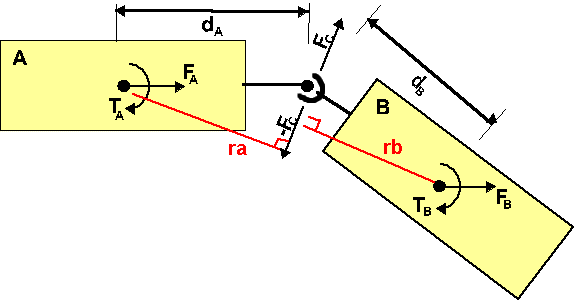
There are no other external forces acting on the system. A force may be transmitted between the two masses Fc (by Newtons third law, the force of b of a is equal and opposite to the force of a on b. There is no torque between the two masses since a hinge is used.
Therefore the dynamics equations are:
{Fa} + {Fc} = ma * {aa}
{Fb} - {Fc} = mb * {ab}
| where: | |||
symbol |
description |
type |
units |
| {Fa} | external force on mass 'a' | vector | N=newton=kg*m/s2 |
| {Fb} | external force on mass 'b' | vector | N=newton=kg*m/s2 |
| {Fc} | force transmitted between hinge | vector | N=newton=kg*m/s2 |
| ma | mass of 'a' | scalar | kg |
| {aa} | linier acceleration of 'a' | vector | m/s2 |
| mb | mass of 'b' | scalar | kg |
| {ab} | linier acceleration of 'b' | vector | m/s2 |
Newtons second law, applied to angular momentum, the net extenal torque
acting on a system equals the rate of change of the angular momentum of
the system. Angular momentum L=Iw and T=I![]() .
.
Assume we are working in the frame of reference of object 'a'. Therefore we can use the following equations (from dynamics 1 - case 2)
Tax = Iaxx aax
Tay = Iayy aay
Taz = Iazz aaz


