On this page we derive the rotation values from a point mass (particle). The point mass is not necessarily rotating about its own axis (although it could, subatomic paricles have spin). What we are interested in here is the contribution of the particle to the rotatinal properties of a bigger mass about some fixed point. If I am not making myself very clear try reading numerical methods.
The following pages will then go on to derive quantities for finite solid bodies by integrating across the volume. Most of these quantities are vectors of dimension 3 which has a component in the x,y and z directions. To denote a vector quantity we show an arrow above the quantity, for more information about vectors see here.
Angular Acceleration of particle (α)
The linear acceleration of a particle on a solid body due to circular motion is:
=
a0 + α × 
+ w × (w × )
| where: | |||
symbol |
description |
type |
units |
|
linear acceleration of particle on a solid body | vector | m/s2 |
| a0 | linear acceleration of centre of mass of solid body | vector | m/s2 |
| α | angular acceleration of solid body | bivector | s-2 |
| × | cross multiplication | ||
|
position of particle relative to centre of mass | vector | m |
| w | angular velocity of solid body | bivector | s-1 |
As you can see from the equation it is made up of three parts, a linear acceleration due to the acceleration of the centre of mass and there are two parts due to the rotation as described here:
- A linear acceleration due to centrifugal force|.
- A linear acceleration due to any change in angular velocity
- A linear acceleration due to the acceleration of the centre of mass.
Let us take a specific case, imagine that the particle is traveling in a circle
around point 
.
So in this case the linear acceleration will be made up of two components:
- A linear acceleration due to centrifugal force, which is of magnitude w
x (w x ).
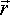The direction is toward the centre of the orbit, since w and r are at 90 degrees
to each other this gives -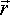 * |w2|.
- A linear acceleration due to any change in angular velocity d
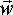/dt
x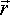
In the above example I have shown the centre of the circle of rotation ,
and the point that we are measuring the angular acceleration about 1,
as being separate points.
But if we take the special case where we are measuring the angular acceleration
about the centre of the circle of rotation, then the centrifugal acceleration
is in the same direction as so the cross product is zero. So, in this case only, we only need to consider 
=
d/DT
Part due to angular acceleration
linear acceleration is the cross product of its angular acceleration, about a point, the with its distance from the point.
=
α
x 1
| where: | |||
symbol |
description |
type |
units |
| α | the instantaneous angular acceleration about Pc1 | bivector | radians s-2 |
| x | x is the cross product operator (see here for definition) | ||
| 1 |
the instantaneous position of the particle relative to point.  -1 |
vector | m |
|
the instantaneous linear acceleration about Pc1 | vector | m/s2 |
Let us take a specific case, imagine that the particle is traveling in a circle
around point .
So in this case the linear acceleration will be made up of two components:
- A linear acceleration due to centrifugal force, which is of magnitude rw^2 and with a direction toward the centre of the orbit.
- A linear acceleration due to any change in angular velocity x d/DT
In the above example I have shown the centre of the circle of rotation ,
and the point that we are measuring the angular acceleration about 1,
as being separate points.
But if we take the special case where we are measuring the angular acceleration
about the centre of the circle of rotation, then the centrifugal acceleration
is in the same direction as so the cross product is zero. So, in this case only, we only need to consider
α=
d/dT
Representing Angular Acceleration in program
Angular acceleration in 3D space can be held in a quaternion (see class sfrotation) or a matrix (see class sftransform). For an example of how this might be used in a scenegraph node, see here.
