Physics - Kinematics - Linear Acceleration

If an object is moving at a constant acceleration (as it would be if acted on by a constant force see forces )

Its acceleration is given by:

a = dv / dT

or integrating:

v = ∫a dT

In the more general case of translation in 3 dimensions:

[a] =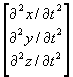

Constant Acceleration (constant force)

If acceleration is constant, which happens when force is constant, so it is a common occurrence, for example when a body is falling in a gravity field.

These equations for uniform acceleration can be solved analytically to give the following equations which relate p, p₀, v, v₀, t and a in different ways:

• v = v₀ + a*t
• p = p₀ + v₀ t + ½ a t²
• v² = v₀² + 2 * a * p

where:		other definitions
symbol	description	type	units
v0	initial velocity	vector	m/s
v	final velocity	vector	m/s
a	acceleration constant	vector	m/s2
t	time	scalar	s
p	final position	vector	m
p 0	position at t=0	vector	m

These equations can be derived using calculus as follows:

Velocity is the rate if change of position:

a = dv/dt

So integrating both sides gives:

v = ∫a dt

so if a is constant:

v = v₀ + a*t

I seem to remember that when I was at school this was written as:

v = u + a t

So integrating acceleration once gives the velocity, to get the position we need to integrate again:

p = ∫v dt

p = ∫(v₀ + a*t) dt

p = p₀ + v₀ t + ½ a t²

Variable Acceleration - approximate methods

If we have an equation for the acceleration, as a function of time, we can apply integration to find the velocity and position, if we don't then we can use approximate methods such as finite difference method, Eulers Method or Runge-Kutta Method. If we are animating a computer simulation then this can be a very good method because we need to generate the position for each frame anyway, so is is much easier to generate the next frame from the frame before it.

v_n+1 = v_n + a * dt

where:		other definitions
symbol	description	type	units
vn+1	velocity at frame n+1	vector	m/s
vn	velocity at frame n	vector	m/s
a	acceleration	vector	m/s2
dt	time between frame n and frame n+1	scalar	s

and summing again:

p_n+1 = p_n + v_n * dt

where:		other definitions
symbol	description	type	units
pn+1	position at frame n+1	vector	m
pn	position at frame n	vector	m
vn	velocity at frame n	vector	m/s
dt	time between frame n and frame n+1	scalar	s

These approximations can be made more accurate by using Eulers Method or Runge-Kutta Method

Representing Acceleration in program

Acceleration in 3D space can be held in a 3D vector (see class sfvec3f). For an example of how this might be used in a scenegraph node, see here.

EuclideanSpace

home

Calculus