Physics - Kinematics - Combined Linear and Angular Velocity

Particle on solid body 2D case

The velocity of the centre of mass is given by Vcm (see linear case)

The velocity of a particle on the solid body, relative to the centre of mass, is given by:

Vpx	=	-ry w
Vpy	=	rx w

(see angular case)

So, combining these, the absolute value of the velocity of a point on a solid body is given by:

Vpx	=	Vcmx - ry w
Vpy	=	Vcmy + rx w

where:

• Vpx = velocity of chosen particle (x component) in absolute coordinates.
• Vpy = velocity of chosen particle (y component) in absolute coordinates.
• Vcmx = velocity of centre of mass (x component) in absolute coordinates.
• Vcmy = velocity of centre of mass (y component) in absolute coordinates.
• rx = position of chosen particle relative to the centre of mass (x component).
• ry = position of chosen particle relative to the centre of mass (y component).
• w = angular velocity (scalar quantity in 2D case)

Note that, since the object is rotating, the vector r will be a function of time:

rx	=	|r| * cos(wt)
ry	=	|r| * sin(wt)

Particle on solid body 3D case

The velocity of the centre of mass is given by Vcm (see linear case)

The velocity of a particle on the solid body, relative to the centre of mass, is given by:

= ×

where:		other definitions
symbol	description	type	units
	instantaneous linear velocity of particle	vector	m/s
	instantaneous angular velocity about . (dθ/dt)	bivector	s-1
	instantaneous position of the particle relative to point. -	vector	m
×	vector cross product operator (see here for definition)

This can be shown as follows:

Assuming that rotation is in the direction of the positive z dimention (since we are using right hand coordinates this is toward the viewer). Also since we are using right hand screw rule for positive rotation this will be an anti-clockwise rotation so, dividing the velocity into components in x and y directions, we get:

situation when at top of rotating object	situation when at right of rotating object
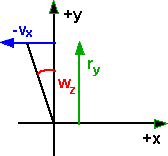vx = -wz * ry	vy = wz * rx

If we consider components rotating about other axes then we get:

v_x = w_y * r_z -w_z * r_y
v_y = w_z * r_x- w_x * r_z

If we also consider the component in the z direction then we get the general expression for linear velocity on a rotating body (you can check this by using the expression for a cross product here):

= ×

note: the above uses:

• right hand coordinate system.
• right hand rule for positive rotations.
• right handed cross product convention.

If we change any one of these to a left hand rule then the order of the operands will be reversed, since × = -(×), but if we change two of them (left hand coordinate system and left hand rule for positive rotations) then the above equation still applies.

For a solid body

Combining the linear and rotational cases, the absolute value of the velocity of a point on a solid body is given by:

Vp = Vcm + wx r

where:

• Vp = velocity of chosen particle (vector) in absolute coordinates.
• Vcm = velocity of centre of mass (vector) in absolute coordinates.
• r = position of chosen particle relative to the centre of mass (vector).
• w = angular velocity (vector quantity in 3D case)

Note that, since the object is rotating, the vector r will be a function of time.

Particle on solid body 3D using Matrix

I would like to derive the equations of motion and ultimately the collision equations in terms of matrices. This might have advantages in that it would fit in with the inertia tensor, also it would be useful to separate out a 'state vector' which defines the state of the solid body (angular and linear position and velocity).

So the velocity of a particle on a solid body is given by:

Vpx Vpy Vpz

=

1 0 0 0 -rz ry 0 1 0 rz 0 -rx 0 0 1 -ry rx 0

Vcmx Vcmx Vcmx wx wy wz

The rotational part of this matrix was derived by replacing the vector cross product with the equivalent skew symmetric matrix.

Since r is dependant on the orientation of the body we could further extend the right hand vector to include the orientation, then the central matrix could be made completely independent of the state of the solid body. The idea is that, if we were writing a game which has a lot of solid bodies moving around we could represent them by an array holding all the state vectors, the central matrix would then define the physics and be independent of the state of each solid body.

However, I am not sure how to represent the orientation in the state vector?

• euler angles? - hard to combine rotations - calculating position requires lots of trig functions (sine, cosine, etc.)
• quaternions? - physics equations can be difficult to write in terms of quaternoins
• matrix? - does not really fit in vector

I think quaternoins might be best? but could we use it in matrix form like this?:

can anyone help me with this?

Vpx Vpy Vpz

=

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

qx qy qz qw Vcmx Vcmx Vcmx wx wy wz

I dont think we can do this because to express an absolute position (P2) in terms of a position in local body coordinates (P1) and orientation as a quaternion (qw,qx,qy,qz) we need an equation like this (which is not linear):

EuclideanSpace

home

Standards

Linear Functions

Vector Cross Product