 |
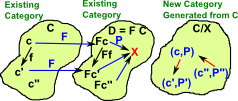
On a previous page we looked at ways to construct categories from existing categories. On this page we look at how objects in existing categories can become arrows in a new category. |
A specific case of arrow categories is comma categories and a more specific case is slice categories. We can then further generalise to pullbacks.
In some circumstances we will see that certain universal properties are conserved.
Here are some examples of comma categories. In these cases all the objects are in the same category (including the fixed object). The comma category generalises this by allowing the objects to come from other categories.
Arrow categorysee page here |
 |
|
Examples |
Slice categorysee page here |
 |
|
|
Co-slice categorysee page here |
 |
|
Examples |
Arrow Category
 |
The arrow category gives us a way to convert objects into arrows. |
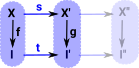
| objects: | f: X -> I | Objects in this arrow category are arrows between two categories. To specify this completely we need a triple <X,I,f> consisting of the two objects and the morphism between them. | ||
| morphisms: | <s,t> | where 's' is an arrow in the source and 't' is an arrow in the target. |
where the above diagram commutes, that is:
g•s = t •f
Inside Functors
Page about functors here. A functor maps both elements and functions in some category.
In category theory we don't tend to look inside categories (such as the category of set). However I find it helps my intuition to attempt to derive properties of some categories (such as arrow category) from internal properties.
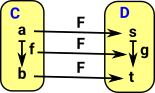 |
The mapping of functions must play well with the mapping of the elements. g•F= F•f or since g = F f : (F f) • F= F•fwhere • represents function composition. |
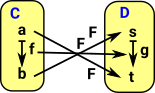 |
Or we could have a contravarient functor: (Ff)-1 • F = F •f |
An alternative approach could be, rather than looking at an individual functor, we could try to look at all possible functions in terms of homsets:
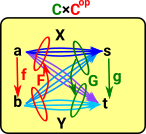 |
|---|
This can lead to structure in:
- Comma and arrow categories.
- Pre-sheaf, sheaf and Yoneda lemma.
- Fibrations and Grothendiek construction.
Co-fibration
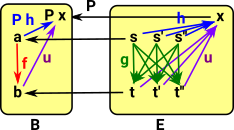
Where:
|
When we try to reverse the projection P then:
|
Comma Category
The comma category is like an arrow catagory but the source and target may be specified as functors from other categories. See page here.
Related Categories