Introduction
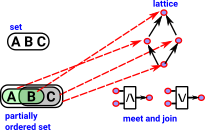
A model category has similarities to the category of sets except the morphisms are continuous. See page here for discussion of continuous functions.
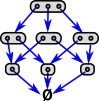
It has three classes of morphisms:
in the same way that set has bijections, surjections and inclusions.
Mappings in Model Categories
Having looked at the above structures in set we can now look at related structures in model categories.
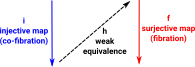
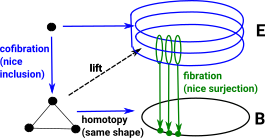
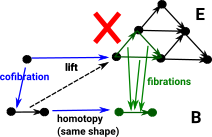
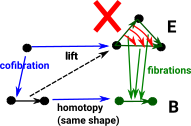
The weak equivalences are ‘homotopy equivalences’ that is shapes that can be deformed into each other. They are 'weak' because they are spaces that can be represented by simplicial sets, that is there are no awkward singularities or things like that which may be possible in more general case (see: Warsaw circle - ncatlab).
The fibrations are Serre fibrations and play the role of ‘nice surjections’. For a general discussion about fibrations see the page here.
The cofibrations play the role of ‘nice inclusions’ see the page here.
Decomposition of Mappings in Model Categories
Mappings in model categories are continuous and can be decomposed into weak equivalences, fibrations and cofibrations. |
 |
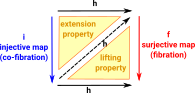 |
These mappings commute giving the extension property and the lifting property.
|
Lifting Property in Topology
This fibration is like a fibre bundle in sets, the differences are:
That is: the fibration goes from E to B (the vertices map in that direction) but the open sets map in the other direction so if we first map each point to an open set containing only that point we can then map to E. So composing these arrows gives 'lift'. |
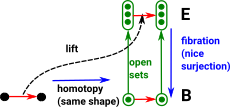 |
For more about the lifting property see the page here.
Homotopy Extension Property (HEP)
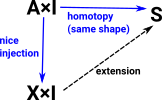 |
Given a homotopy of maps from A to S and an injection from A into a bigger space X (A is a subspace of X) |
|
Example for showing open sets mapping in the opposite direction. |
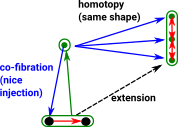 |
This is the inverse of the lift property.
For more about the extension property see the page here.
Lifting and Extension Properties
All arrows (mappings) are continuous. If the square commutes then the dotted arrow (lift) must be unique. Where:
|
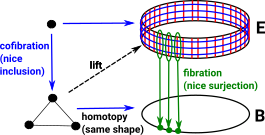 |
So if the blue circles in E are equal at one point, they are equal everywhere (we cant have a tear in topology.
Here we see, although B is a circle here, p-1(b) does not need to be the same shape. |
 |
Path Lifting |
 |
| The lifted paths in E must either agree at every point or at no points, lift is unique, we cant have a tear in the topology. So the diagram on the right is not valid. | 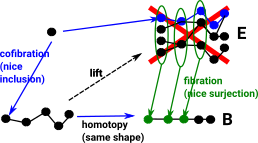 |
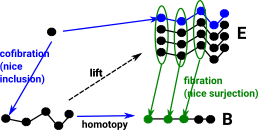
| Can we apply this to higher dimensional spaces and simplicial complexes? | 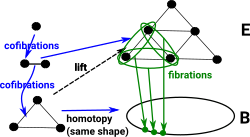 |
It doesn't seem to work for finite lines (edges) in a complex (graph in this case). E is not a topological space, mapping of edges onto singe edge doesn't seem to be a fibration and picking out a point (node) doesn't seem to identify a single edge. |
 |
What if we restrict to the inside of a single simplex? Here the triangle 'E' is filled in so two of the edges can continuously merge together. It still doesn't seem to work. It seems that the fibration is not a surjection, perhaps we need to think of it more like a projection. |
 |
see: https://en.wikipedia.org/wiki/Fibration_of_simplicial_sets
Simplicial Set ExampleHere we have two triangles 1 and 2 with a common edge 3. The relationship between triangles, lines (edges) and points (vertex) is many to many. For example, edge 3 is contained in multiple trianges and each triangle has multiple edges. |
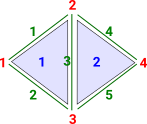 |
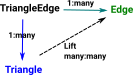
| If we were representing many:many relationships between tables in a relational database we insert tables between them with 1:many relationships out of them. |  |
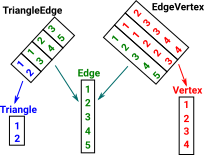 |
The new table 'TriangleEdge' is redrawn here a bit so both the 1:many relations coming out of it look like projections. The same for table 'EdgeVertex' |
| From this we can recalculate the tables so the arrows go in one direction: triangle->edge->vertex. | 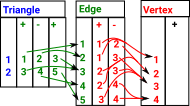 |
 |
Retractions
A retraction is a surjective map that is continuous. For instance we can continuously reduce a band down to a circle: |
 |
| In general a map ƒ: M1 -> M2 is continuous if and only if the preimage of every open set is open. |
Model Category in CTT
We have some nice properties if mappings are continuous. The most general form of continuous map is mapping between topological spaces where all open sets in codomain have preimage which is an open set. However, lines are not open sets in general. To get these properties we need to restrict to structures where we do have these properties such as maps between simplicies.
Fibration in CTT
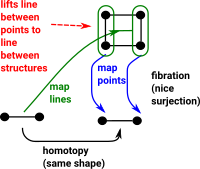
A fibration allows us to 'lift' a line between two points to a line between two structures. This is called the homotopy lifting property (HLP). In this diagram the blue lines show the mapping of points and the green line maps lines (like open set) in the opposite direction to the points. |
 |
Cofibration in CTT
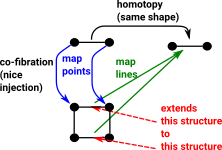
A cofibration allows us to 'extend' a mapping from a subset to a mapping from the whole structure. This is called the homotopy extension property (HEP). Again the blue lines show the mapping of points and the green line maps lines (like open set) in the opposite direction to the points. |
 |
Kan Fibration
Kan fibrations are the fibrations of the standard model category structure on simplicial sets (see wiki)
A Kan fibration need not be a surjection (ncatlib)
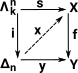
x must exist where:
|
 |
| Example where n=2 (triangle - two dimensional). | 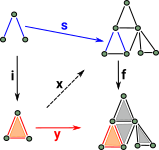 |
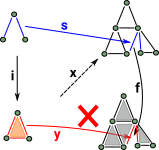 |
We need the outer square to commute so that we can't have a situation like this. |
| Example where n=1 (line - one dimensional). | 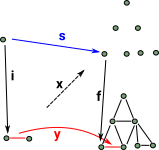 |
Continuation of Simplicial Set ExampleIn the example above the two triangles 1 and 2 were 'glued' together with a common edge 3. |
 |
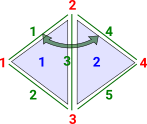 |
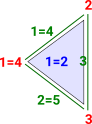
What if we now 'glue' together two more edges, say 1 and 4? |
This would force edge 2 to equal edge 5 and effectively make the two triangles equal. Can we generalise this to determine how many faces need to be glued together to make two simplicies equal? |
 |
Fibration and Co-fibration
Homotopy has the concept of:
- a fibration which has the lifting property.
- a co-fibration which has the extension property -extension is dual to lift.
Fibration |
Co-fibration (Extension Property) |
|
|---|---|---|
| Homotopy | Fibration |
Co-fibration (see page here) |
Combinatorics |
Kan fibration (see page here) |
Kan extension (see page here) |
Kan fibrations are combinatorial analogs of Serre fibrations of topological spaces.
(ncatlab).
Extension is dual to lift.
Fibrations and Cofibrations are used in model theory.