In order to treat a function as a type it must hold all possible mappings. An instance of that is an individual mapping.
The hom-set is the set of possible functions/mappings/morphisms between a domain and codomain.
Hom-Set in Sets
In sets between a domain set with A elements to a codomain set with X elements denoted A -> X there are XA possible mappings. In the example (diagram right) between a domain set with 2 elements to a codomain set with 3 elements there are 32 = 9 possible mappings. |
 |
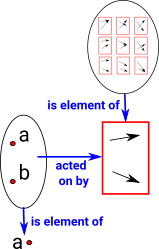 |
An element of the homset acts on a whole object. So the homset is above the level of functions and objects. |
Hom-Set as a type
In type theory, types can be things such as Integer, Real (Float in computing), Boolean etc. In addition to these types a function can also be a type such as Integer -> Boolean can also be a type. This type is a hom-set, it consists of a set of possible functions such as:
- x < 0
- x² < 16
- and so on ...
As we can se fro the diagram above each element of the hom-set is a function and each of these functions operates on a complete set. So we have a 3-layer hierarchy:
- A complete hom-set.
- An individual function from that hom-set.
- An individual element in the domain which maps to an individual element in the codomain.
So the middle layer relates to an element in the set of functions but the whole 'set' in the domain/codomain.
The equation:
a(b+c) = ab ac
where a,b and c are types, also suggests a way of going between whole sets and elements of a set.
Hom-Set in Category Theory
If C is a category containing objects A and B then Hom(A,B) is the collection of all morphisms from A to B:
Hom(A,B) = {f![]() C | f: A -> B }
C | f: A -> B }
where:
- A = Dom(f)
- B = Cod(f)
Internal Hom-Set
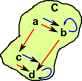 |
Many types of category can be represented by a graph which can be shown as a set of objects and a set of arrows. The graph of one (red) endofunctor might be represented by:
and the other (blue) endo functor by
|
|||
| In category theory we try to define things using their external properties. So the set of morphisms could be shown externally. |
External Hom-Set
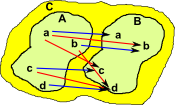 |
Here the morphism goes from object A to object B as suggested by the general definition at the top of the page. |
 |
Again, in category theory, we try to define things using their external properties. So the set of morphisms could be shown externally. |
Relation to Exponential Object
An internal hom-set in a cartesian closed category is an exponential object.
homC(Z,XY) = homC(Z×Y,X)
Representable Functor
We can map objects of a category to functors (represented by a homset) like this:
| HA = C(A,-) | is a contravarient representable at A |
| HA = C(-,A) | is a covarient representable at A |
where:
- C(A,-) means B -> C(A,B)
- C(-,A) means B -> C(B,A)
That is, the dash '-' represents what we are mapping from.
more about representable functor here.
Composing Homsets
Homsets can be composed:
hom(y,z)![]() hom(x,y)->hom(x,z)
hom(x,y)->hom(x,z)
Enriched Categories
So far diagrams on hom-sets are valid upto equality, usually in category theory diagrams are upto isomorphism.
Programming
The sage program (see this site) can operate on hom-sets like this:
sage: V = VectorSpace(QQ,3) sage: Hom(V, V)
Set of Morphisms from Vector space of dimension 3 over Rational Field to Vector space of dimension 3 over Rational Field in Category of vector spaces over Rational Field
sage: G = AlternatingGroup(3) sage: Hom(G, G)
Set of Morphisms from AlternatingGroup(3) to AlternatingGroup(3) in Category of finite permutation groups
sage: Hom(ZZ, QQ, Sets())
Set of Morphisms from Integer Ring to Rational Field in Category of sets
sage: Hom(FreeModule(ZZ,1), FreeModule(QQ,1))
Set of Morphisms from Ambient free module of rank 1 over the principal ideal domain Integer Ring to Vector space of dimension 1 over Rational Field in Category of modules with basis over Integer Ring
sage: Hom(FreeModule(QQ,1), FreeModule(ZZ,1))
Set of Morphisms from Vector space of dimension 1 over Rational Field to Ambient free module of rank 1 over the principal ideal domain Integer Ring in Category of vector spaces over Rational Field