Tensors allow us to define fields and transformations in a way that is independent of coordinate systems. We can use curvilinear coordinate systems and tensors allowed Einstein to formulate special relativity.
Tensors are scalars, vectors, matrices and hypermatricies which are multilinear (not every hypermatrix is multilinear but vectors and matrices always are).
As usual I'll start with the different ways to approach the subject. It often seems to be the case with these powerful mathematical concepts that we can think of them in different ways:
- As multilinear mappings.
- As objects which extend matrices so that the elements can be addressed by an arbitrary number of indicies.
- As a way to describe geometrical properties in different coordinate systems.
- As a way to describe the properties of manifolds.
- As a way to describe symmetries (related to group theory)
In order to be a tensor, a quantity needs to be a multilinear. It changes, according to certain rules, in response to a change of frame.
In this subject, even more than most, there seem to be different definitions of the concepts. If you are reading different articles and books it is important to compensate for the different ways that things are defined. One of the differences is whether a tensor is defined as a mapping, such as when mapping from one coordinate system to another. Alternatively a tensor can be defined as a particular field such as how an electromagnetic field varies in space, this is the approach usually taken by physicists.
Another difference is whether tensors are defined in terms of incidies, a coordinate based approach or whether an approach independent of coordinates is used. The latter approach is considered more modern but it may be harder to learn and may not handle all situations. These pages use the first approach. The Geometric Algebra pages also use a coordinate free approach and, is complimentary to this subject.
Multilinear mappings
When we looked at vectors we saw that they are linear as described by the 'distributivity law':
| c(v1 + v2) = c v 1 + c v2 | where v 1 and v2 are vectors and c is a scalar. |
A key property of tensors is that they generalise this linearity to the concept of multilinear, that is being linear in many variables.
Tensors can be used to represent multilinear mappings (such as transformations) in 'n' dimensions. Physicists also use tensor fields to map each point in space (manifold) to a tensor (such as scalar or vector) value.
A simple example of a linear transform might be:
x' = 3*x + 4*y
y' = 5*x + 3*y
Which could, of course, be represented by a matrix equation. In geometric terms this could be interpreted as mapping points (x,y) to another set of points (x',y'). Alternatively it could be interpreted as representing the same point in different coordinate systems.
This subject is often concerned with mapping between different coordinate systems and also the properties which are independent of coordinate systems.
Although tensors can represent general (multi-) linear mappings most of the complexity and power of the subject seems to come when we constrain the tensors to represent various types of symmetry.
There are two approaches to tensors:
- Classical Approach - We can use an approach and based on a fixed frame of reference (coordinate system or basis) the notation for this uses indicies based on the coordinate system. this uses "components" which are elements in the array.
- Modern Approach - We can use an approach which is independent of the coordinate system and is component free.
Classical Approach
In classical terms concept of tensors is defined by an array of components in such a way that it can be used in any number of dimensions and any 'rank'. Where:
- Rank: is the number of indicies required to determine the component, as shown in the following table:
- Dimension: is the range of each of the indicies.
rank |
representation |
| 0 | scalar |
| 1 | vector |
| 2 | matrix (n * vectors) |
| 3 | hyper-matrix |
We tend to use two types of indicies to distinguish between contravariant and covariant indicies.
- contravariant indicies - shown as superscripts - components vary contravariant with respect to a change in the frame of reference.
- covariant indicies - shown as subscripts - components vary covariant with respect to a change in the frame of reference.
Grade 1 Tensors - Vectors
In order to give a vector a definate value we need to assign numerical values to it. To do this it can be represented by a linear combination of basis vectors, so vector 'a' could be represented by:
a = a1 e1 + a2 e2 + a3 e3 ...
simarly vector 'b', in the same coordinate system, could be represented by:
b = b 1 e1 + b 2 e2 + b 3 e3 ...
where:
- a and b = vectors being defined
- a1 ,a2 , a3 , b1 ,b2and b3 = scalar values
- e1 , e2 and e3= common vector bases
Grade 2 Tensors - Matricies
Terminology
Dual vectors
- reflects the relationship between row vectors and column vectors
- when multiplied by its corresponding vector, generate a real number, by systematically multiplying each component from the dual vector and the vector together and summing the total. If the space a vector lives in is shrunk, a contravariant vector shrinks, but a covariant vector gets larger.
In the way that tensors are 'n' dimensional and also in the way that they are developed and used by physicists they are related to spinors.
There also seems to be a relationship to Clifford / Geometric algebra, if only the terminology used. Is this just a coincidence? or is there some higher truth here?
Tensors
A set of components that obeys some transformation law in n-dimentional space.
A set of components - each of which is defined as a function of position in some co-ordinate system - which obeys some given transformation law.
They are arrays of numbers, or functions, that transform according to certain rules under a change of coordinates.
Tensors were originally used in physics
A tensor may be defined at a single point or collection of isolated points of space (or space-time), or it may be defined over a continuum of points. In the latter case, the elements of the tensor are functions of position and the tensor forms what is called a tensor field. This just means that the tensor is defined at every point within a region of space (or space-time), rather than just at a point, or collection of isolated points.
| Order (or rank) | Mathmatical Representation | Physics Application |
| 0 | Scalar | An example of a scalar field would be the density of a fluid as a function of position |
| 1 | Vector | An example of a vector field is provided by the description of an electric field in space. |
| 2 | Matrix | inertia matrix |
| 3 | ||
| 4 | Riemann curvature tensor |
Note, not all transforms and not all matricies are tensors. To be a tensor they must transform according to certain rules under a change of coordinates.
For instance objects called spinors. Spinors differ from tensors in how the values of their elements change under coordinate transformations. For example, the values of the components of all tensors, regardless of order, return to their original values under a 360-degree rotation of the coordinate system in which the components are described. By contrast, the components of spinors change sign under a 360-degree rotation, and do not return to their original values until the describing coordinate system has been rotated through two full rotations = 720-degrees.
The tensor notion is quite general, and applies to all of the above examples; scalars and vectors are special kinds of tensors. The feature that distinguishes a scalar from a vector, and distinguishes both of those from a more general tensor quantity is the number of indices in the representing array. This number is called the rank of a tensor. Thus, scalars are rank zero tensors (no indices at all), and vectors are rank one tensors.
A tensor may vary covariantly with respect to some variables and contravariantly with respect to others when the coordinate axes are rotated.
Covariant and Contravariant Tensors
A tensor may be Contravariant or Covariant depending on how the corresponding numbers transform relative to a change in the frame of reference
Contravariant indices are written as superscripts, covariant indices are written as subscripts.
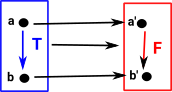
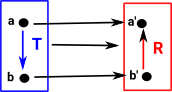
A 'functor' is a function which not only maps objects but it also maps operations (in this case transformations). These transformations must be consistent with the overall function, this can happen in two ways: covarience or contravarience:
| Covarience | Contravarience | |
|---|---|---|
 |
 |
|
| Here the transform F goes down (in the same direction as T) | Here the transform R goes up (in the opposite direction as T) |
Covectors can be contravarient like this:
Imagine we have a point 'a', represented by a vector giving its position as an offset from the origin. This point is transformed by a matrix 'T' to the point 'b'. We can create a transform which goes in the reverse direction (from b to a) by mapping these points to a scalar value 's' (see 'representable functor'). This mapping from point to scalar can be represented by a covector. |
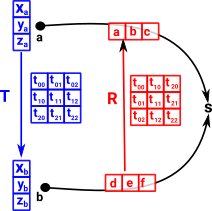 |
We can choose some value for d,e,f to make 's' some value, say 3. So what value do we have to make a,b,c to give the same scalar value? |
|
| We can just compose the arrows in the above diagram or substitute in the equation like this: | 3 = |
|
|
So we have an arrow which goes from d,e,f to a,b,c so it is contravarient.
Valence of a tensor
The valence of a tensor is the pair (p,q), where:
- 'p' is the number contravariant indices.
- 'q' the number of covariant indices.
Tensor Notation Summary
| notation | example | meaning |
|---|---|---|
| subscript | e1 | coordinate basis |
| superscript | x1 | coordinate value |
| Einstein Summation Convention | eixi=e1x1+e2x2+e3x3=∑eixi | When the same index appears twice in an expression, once raised and once lowered, a sum is implied. |
| partial derivatives | ∂a=∂/∂a |
More on notation here.

