Maths - Quaternion to Matrix - Sample Orientations

Sample Rotations

In order to try to explain things and give some examples we can try I thought it might help to show the rotations for a finite subset of the rotation group. We will use the set of rotations of a cube onto itself, this is a permutation group which gives 24 possible rotations as explaned on this page.

rightUp

reference orientation

q = 1

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

1 0 0
0 1 0
0 0 1

 

backUp

rotate by 90 degrees about y axis

q = 0.7071 + j 0.7071

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 0 1
0 1 0
-1 0 0

 

leftUp

rotate by 180 degrees about y axis

q = j

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

-1 0 0
0 1 0
0 0 -1

 

forwardUp

rotate by 270 degrees about y axis

q = 0.7071 - j 0.7071

(equivilant rotation to:
-0.7071 + j 0.7071)

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 0 -1
0 1 0
1 0 0

 

Then apply attitude +90 degrees for each of the above: (note: that if we went on to apply bank to these it would just rotate between these values, the straight up and streight down orientations are known as singularities because they can be fully defined without using the bank value)

upLeft

q = 0.7071 + k 0.7071

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 -1 0
1 0 0
0 0 1

 

 

 

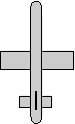
upForward

q = 0.5 + i 0.5 + j 0.5 + k 0.5

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 0 1
1 0 0
0 1 0

 

 

 

upRight

q = i 0.7071 +j 0.7071

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 1 0
1 0 0
0 0 -1

 

 

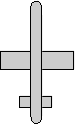
upBack

q = 0.5 - i 0.5 - j 0.5 + k 0.5

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 0 -1
1 0 0
0 -1 0

 

 

 

Or instead apply attitude -90 degrees (also a singularity):

downRight

q = 0.7071 - k 0.7071

(equivilant rotation to:
-0.7071 + k 0.7071)

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 1 0
-1 0 0
0 0 1

 

downBack


q = 0.5 - i 0.5 + j 0.5 - k 0.5

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 0 1
-1 0 0
0 -1 0

 

downLeft

q = -i 0.7071 + j 0.7071

(equivilant rotation to:
i 0.7071 - j 0.7071)

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 -1 0
-1 0 0
0 0 -1

 

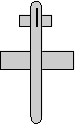
downForward

q = 0.5 + i 0.5 - j 0.5 - k 0.5

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 0 -1
-1 0 0
0 1 0

 

Normally we dont go beond attitude + or - 90 degrees because thes are singularities, instead apply bank +90 degrees:

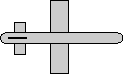
rightForward

q = 0.7071 + i 0.7071

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

1 0 0
0 0 -1
0 1 0

 

 

backRight

q = 0.5 + i 0.5 + j 0.5 - k 0.5

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 1 0
0 0 -1
-1 0 0

 

 

leftBack

q = j 0.7071 - k 0.7071

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

-1 0 0
0 0 -1
0 -1 0

 

forwardLeft

q = 0.5 + i 0.5 - j 0.5 + k 0.5

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 -1 0
0 0 -1
1 0 0

 

 

Apply bank +180 degrees:

rightDown

q = i

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

1 0 0
0 -1 0
0 0 -1

 

backDown

q = i 0.7071 - k 0.7071

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 0 -1
0 -1 0
-1 0 0

 

leftDown

q = k

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

-1 0 0
0 -1 0
0 0 1

 

forwardDown

q = i 0.7071 + k 0.7071

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 0 1
0 -1 0
1 0 0

 

Apply bank -90 degrees:

rightBack

q = 0.7071 - i 0.7071

(equivilant rotation to:
-0.7071 + i 0.7071)

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

1 0 0
0 0 1
0 -1 0

 

backLeft

q = 0.5 - i 0.5 + j 0.5 + k 0.5

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 -1 0
0 0 1
-1 0 0

 

leftForward

q = j 0.7071 + k 0.7071

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

-1 0 0
0 0 1
0 1 0

 

 

forwardRight

q = 0.5 - i 0.5 - j 0.5 - k 0.5

1 - 2*qy2 - 2*qz2 2*qx*qy - 2*qz*qw 2*qx*qz + 2*qy*qw
2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz2 2*qy*qz - 2*qx*qw
2*qx*qz - 2*qy*qw 2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy2

 

0 1 0
0 0 1
1 0 0

 
metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

cover us uk de jp fr caVisualizing Quaternions by Andrew J. Hanson

Other Math Books

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.