Maths - Euler to Axis-Angle - Sample Orientations

Sample Rotations

In order to try to explain things and give some examples we can try I thought it might help to show the rotations for a finite subset of the rotation group. We will use the set of rotations of a cube onto itself, this is a permutation group which gives 24 possible rotations as explaned on this page.

heading applied first giving 4 possible orientations:

rightUp

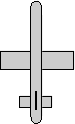
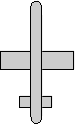
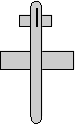
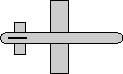
reference orientation

heading = 0
attitude = 0
bank = 0

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =1
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =1
s1 = sin(heading/2) =0
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0

which gives:

angle = 0
x = 0
y = 0
z = 0

Normalise axis, since angle is 0 axis can be anything so set axis to (1,0,0)

angle = 0 degrees
axis = 1,0,0

backUp

rotate by 90 degrees about y axis

heading = 90 degrees
attitude = 0
bank = 0

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =1
s1 = sin(heading/2) =0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0

which gives:

angle = 90 degrees
x = 0
y = 0.7071
z = 0

Normalising axis gives:

angle = 90 degrees
axis = 0,1,0

leftUp

rotate by 180 degrees about y axis

heading = 180 degrees
attitude = 0
bank = 0

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =1
s1 = sin(heading/2) =1
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0

which gives:

angle = 180 degrees
x = 0
y = 1
z = 0

axis is already normalised

angle = 180 degrees
axis = 0,1,0

forwardUp

rotate by 270 degrees about y axis

heading = -90 degrees
attitude = 0
bank = 0

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =1
s1 = sin(heading/2) =-0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0

which gives:

angle = 90 degrees
x = 0
y = -0.7071
z = 0

Normalising axis gives:

angle = 90 degrees
axis = 0,-1,0

or

angle = -90 degrees
axis = 0,1,0

Then apply attitude +90 degrees for each of the above: (note: that if we went on to apply bank to these it would just rotate between these values, the straight up and streight down orientations are known as singularities because they can be fully defined without using the bank value) post multiply above by 0.7071 + k 0.7071 to give:

upLeft

heading = 0
attitude = 90 degrees
bank = 0

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =1
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =0
s2 = sin(attitude/2) =0.7071
s3 = sin(bank/2) =0

which gives:

angle = 90 degrees
x = 0
y = 0
z = 0.7071

Normalising axis gives:

angle = 90 degrees
axis = 0,0,1

upForward

heading = 90 degrees
attitude = 90 degrees
bank = 0

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =0.7071
s2 = sin(attitude/2) =0.7071
s3 = sin(bank/2) =0

which gives:

angle = 120 degrees
x = 0.5
y = 0.5
z = 0.5

Normalising axis gives:

angle = 120 degrees
axis = 0.5774,0.5774,0.5774

upRight

heading = 180 degrees
attitude = 90 degrees
bank = 0

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =1
s2 = sin(attitude/2) =0.7071
s3 = sin(bank/2) =0

which gives:

angle = 180 degrees
x = 0.7071
y = 0.7071
z = 0

axis is already normalised:

angle = 180 degrees
axis = 0.7071,0.7071,0

upBack

heading = -90 degrees
attitude = 90 degrees
bank = 0

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =-0.7071
s2 = sin(attitude/2) =0.7071
s3 = sin(bank/2) =0

which gives:

angle = 120 degrees
x = -0.5
y = -0.5
z = 0.5

Normalising axis gives:

angle = 120 degrees
axis = -0.5774,-0.5774,0.5774

Or instead apply attitude -90 degrees (also a singularity): post multiply top row by 0.7071 - k 0.7071 to give:

downRight

heading = 0
attitude = -90 degrees
bank = 0

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =1
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =0
s2 = sin(attitude/2) =-0.7071
s3 = sin(bank/2) =0

which gives:

angle = 90 degrees
x = 0
y = 0
z = -0.7071

Normalising axis gives:

angle = 90 degrees
axis = 0,0,-1

(equivilant rotation to:
angle = -90 degrees
axis = 0,0,1)

downBack

heading = 90 degrees
attitude = -90 degrees
bank = 0

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =0.7071
s2 = sin(attitude/2) =-0.7071
s3 = sin(bank/2) =0

which gives:

angle = 120 degrees
x = -0.5
y = 0.5
z = -0.5

Normalising axis gives:

angle = 120 degrees
axis = -0.5774,0.5774,-0.5774

downLeft

heading = 180 degrees
attitude = -90 degrees
bank = 0

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =1
s2 = sin(attitude/2) =-0.7071
s3 = sin(bank/2) =0

which gives:

angle = 180 degrees
x = -0.7071
y = 0.7071
z = 0

axis is already normalised:

angle = 180 degrees
axis = -0.7071,0.7071,0

downForward

heading = -90 degrees
attitude = -90 degrees
bank = 0

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =-0.7071
s2 = sin(attitude/2) =-0.7071
s3 = sin(bank/2) =0

which gives:

angle = 120 degrees
x = 0.5
y = -0.5
z = -0.5

Normalising axis gives:

angle = 120 degrees
axis = 0.5774,-0.5774,-0.5774

Normally we dont go beond attitude + or - 90 degrees because thes are singularities, instead apply bank +90 degrees: post multiply top row by 0.7071 + i 0.7071 to give:

rightForward

heading = 0
attitude = 0
bank = 90 degrees

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =1
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =0
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0.7071

which gives:

angle = 90 degrees
x = 0.7071
y = 0
z = 0

Normalising axis gives:

angle = 90 degrees
axis = 1,0,0

backRight

heading = 90 degrees
attitude = 0
bank = 90 degrees

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0.7071

which gives:

angle = 120 degrees
x = 0.5
y = 0.5
z = -0.5

Normalising axis gives:

angle = 120 degrees
axis = 0.5774,0.5774,-0.5774

leftBack

heading = 180 degrees
attitude = 0
bank = 90 degrees

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =1
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0.7071

which gives:

angle = 180 degrees
x = 0
y = 0.7071
z = -0.7071

axis is already normalised:

angle = 180 degrees
axis = 0,0.7071,-0.7071

forwardLeft

heading = -90 degrees
attitude = 0
bank = 90 degrees

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =-0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0.7071

which gives:

angle = 120 degrees
x = 0.5
y = -0.5
z = 0.5

Normalising axis gives:

angle = 120 degrees
axis = 0.5774,-0.5774,0.5774

Apply bank +180 degrees: post multiply top row by i to give:

rightDown

heading = 0
attitude = 0
bank = 180 degrees

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =1
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0
s1 = sin(heading/2) =0
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =1

which gives:

angle = 180 degrees
x = 1
y = 0
z = 0

axis is already normalised:

angle = 180 degrees
axis = 1,0,0

backDown

heading = 90 degrees
attitude = 0
bank = 180 degrees

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0
s1 = sin(heading/2) =0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =1

which gives:

angle = 180 degrees
x = 0.7071
y = 0
z = -0.7071

axis is already normalised:

angle = 180 degrees
axis = 0.7071,0,-0.7071

leftDown

heading = 180 degrees
attitude = 0
bank = 180 degrees

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0
s1 = sin(heading/2) =1
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =1

which gives:

angle = 180 degrees
x = 0
y = 0
z = 1

axis is already normalised:

angle = 180 degrees
axis = 0,0,1

forwardDown

heading = -90 degrees
attitude = 0
bank = 180 degrees

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0
s1 = sin(heading/2) =-0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =1

which gives:

angle = 180 degrees
x = 0.7071
y = 0
z = 0.7071

axis is already normalised:

angle = 180 degrees
axis = 0.7071,0,0.7071

Apply bank -90 degrees: post multiply top row by 0.7071 - i 0.7071 to give:

rightBack

heading = 0
attitude = 0
bank = -90 degrees

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =1
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =0
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =-0.7071

which gives:

angle = 90 degrees
x = -0.7071
y = 0
z = 0

Normalising axis gives:

angle = 90 degrees
axis = -1,0,0

(equivilant rotation to:
angle = -90 degrees
axis = 1,0,0)

backLeft

heading = 90 degrees
attitude = 0
bank = -90 degrees

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =-0.7071

which gives:

angle = 120 degrees
x = -0.5
y = 0.5
z = 0.5

Normalising axis gives:

angle = 120 degrees
axis = -0.5774,0.5774,0.5774

leftForward

heading = 180 degrees
attitude = 0
bank = -90 degrees

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =1
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =-0.7071

which gives:

angle = 180 degrees
x = 0
y = 0.7071
z = 0.7071

axis is already normalised:

angle = 180 degrees
axis = 0,0.7071,0.7071

 

forwardRight

heading = -90 degrees
attitude = 0
bank = -90 degrees

angle = 2 * acos(c1c2c3 - s1s2s3)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =-0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =-0.7071

which gives:

angle = 120 degrees
x = -0.5
y = -0.5
z = -0.5

Normalising axis gives:

angle = 120 degrees
axis = -0.5774,-0.5774,-0.5774
metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

cover us uk de jp fr caVisualizing Quaternions by Andrew J. Hanson

Other Math Books

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.