Maths - Axis-Angle to Matrix - Sample Orientations

Sample Rotations

In order to try to explain things and give some examples we can try I thought it might help to show the rotations for a finite subset of the rotation group. We will use the set of rotations of a cube onto itself, this is a permutation group which gives 24 possible rotations as explaned on this page.

In the following table we will need to know what quadrant the results are in, so I have taken some sample results from Math.atan2

heading applied first giving 4 possible orientations:

rightUp

reference orientation

angle = 0 degrees
axis = 1,0,0

  • c =cos(angle) = 1
  • s = sin(angle) = 0
  • t =1 - c = 0
[R] =
t*x*x + c = 1 t*x*y - z*s = 0 t*x*z + y*s = 0
t*x*y + z*s = 0 t*y*y + c = 1 t*y*z - x*s = 0
t*x*z - y*s = 0 t*y*z + x*s = 0 t*z*z + c = 1
1 0 0
0 1 0
0 0 1

backUp

rotate by 90 degrees about y axis

angle = 90 degrees
axis = 0,1,0

 

  • c =cos(angle) = 0
  • s = sin(angle) = 1
  • t =1 - c = 1
[R] =
t*x*x + c = 0 t*x*y - z*s = 0 t*x*z + y*s = 1
t*x*y + z*s = 0 t*y*y + c = 1 t*y*z - x*s = 0
t*x*z - y*s = 1 t*y*z + x*s = 0 t*z*z + c = 0
0 0 1
0 1 0
-1 0 0

 

leftUp

rotate by 180 degrees about y axis

angle = 180 degrees
axis = 0,1,0

 

  • c =cos(angle) = -1
  • s = sin(angle) = 0
  • t =1 - c = 2
[R] =
t*x*x + c = -1 t*x*y - z*s = 0 t*x*z + y*s = 0
t*x*y + z*s = 0 t*y*y + c = 1 t*y*z - x*s = 0
t*x*z - y*s = 0 t*y*z + x*s = 0 t*z*z + c = -1
-1 0 0
0 1 0
0 0 -1

 

forwardUp

rotate by 270 degrees about y axis

angle = 90 degrees
axis = 0,-1,0

or

angle = -90 degrees
axis = 0,1,0

 

  • c =cos(angle) = 0
  • s = sin(angle) = 1 or -1
  • t =1 - c = 1

 

[R] =
t*x*x + c = 0 t*x*y - z*s = 0 t*x*z + y*s = -1
t*x*y + z*s = 0 t*y*y + c = 1 t*y*z - x*s
t*x*z - y*s = 1 t*y*z + x*s = 0 t*z*z + c = 0
0 0 -1
0 1 0
1 0 0

 

Then apply attitude +90 degrees for each of the above: (note: that if we went on to apply bank to these it would just rotate between these values, the straight up and streight down orientations are known as singularities because they can be fully defined without using the bank value)

upLeft

angle = 90 degrees
axis = 0,0,1

  • c =cos(angle) = 0
  • s = sin(angle) = 1
  • t =1 - c = 1
[R] =
t*x*x + c = 0 t*x*y - z*s = -1 t*x*z + y*s =0
t*x*y + z*s = 1 t*y*y + c = 0 t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 -1 0
1 0 0
0 0 1

 

upForward
angle = 120 degrees
axis = 0.5774,0.5774,0.5774

  • c =cos(angle) = 0.866
  • s = sin(angle) = -0.5
  • t =1 - c = 0.134
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 0 1
1 0 0
0 1 0

 

upRight

angle = 180 degrees
axis = 0.7071,0.7071,0

  • c =cos(angle) = -1
  • s = sin(angle) = 0
  • t =1 - c = 2
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 1 0
1 0 0
0 0 -1

 

upBack
angle = 120 degrees
axis = -0.5774,-0.5774,0.5774

  • c =cos(angle) = 0.866
  • s = sin(angle) = -0.5
  • t =1 - c = 0.134
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 0 -1
1 0 0
0 -1 0

 

Or instead apply attitude -90 degrees (also a singularity):

downRight

angle = 90 degrees
axis = 0,0,-1

(equivilant rotation to:
angle = -90 degrees
axis = 0,0,1)

  • c =cos(angle) = 0
  • s = sin(angle) = 1
  • t =1 - c = 1
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 1 0
-1 0 0
0 0 1

downBack

angle = 120 degrees
axis = -0.5774,0.5774,-0.5774

  • c =cos(angle) = 0.866
  • s = sin(angle) = -0.5
  • t =1 - c = 0.134
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 0 1
-1 0 0
0 -1 0

downLeft

angle = 180 degrees
axis = -0.7071,0.7071,0

  • c =cos(angle) = -1
  • s = sin(angle) = 0
  • t =1 - c = 2
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 -1 0
-1 0 0
0 0 -1

downForward

angle = 120 degrees
axis = 0.5774,-0.5774,-0.5774

  • c =cos(angle) = 0.866
  • s = sin(angle) = -0.5
  • t =1 - c = 0.134
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 0 -1
-1 0 0
0 1 0

Normally we dont go beond attitude + or - 90 degrees because thes are singularities, instead apply bank +90 degrees:

rightForward


angle = 90 degrees
axis = 1,0,0

  • c =cos(angle) = 0
  • s = sin(angle) = 1
  • t =1 - c = 1
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c

1 0 0
0 0 -1
0 1 0

backRight
angle = 120 degrees
axis = 0.5774,0.5774,-0.5774

  • c =cos(angle) = 0.866
  • s = sin(angle) = -0.5
  • t =1 - c = 0.134
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 1 0
0 0 -1
-1 0 0

leftBack

angle = 180 degrees
axis = 0,0.7071,-0.7071

  • c =cos(angle) = -1
  • s = sin(angle) = 0
  • t =1 - c = 2
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
-1 0 0
0 0 -1
0 -1 0

forwardLeft

angle = 120 degrees
axis = 0.5774,-0.5774,0.5774

  • c =cos(angle) = 0.866
  • s = sin(angle) = -0.5
  • t =1 - c = 0.134
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 -1 0
0 0 -1
1 0 0

Apply bank +180 degrees:

rightDown

angle = 180 degrees
axis = 1,0,0

  • c =cos(angle) = -1
  • s = sin(angle) = 0
  • t =1 - c = 2
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
1 0 0
0 -1 0
0 0 -1

 

backDown

angle = 180 degrees
axis = 0.7071,0,-0.7071

  • c =cos(angle) = -1
  • s = sin(angle) = 0
  • t =1 - c = 2
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 0 -1
0 -1 0
-1 0 0

 

leftDown

angle = 180 degrees
axis = 0,0,1

  • c =cos(angle) = -1
  • s = sin(angle) = 0
  • t =1 - c = 2
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
-1 0 0
0 -1 0
0 0 1

forwardDown

angle = 180 degrees
axis = 0.7071,0,0.7071

  • c =cos(angle) = -1
  • s = sin(angle) = 0
  • t =1 - c = 2
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 0 1
0 -1 0
1 0 0

Apply bank -90 degrees:

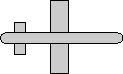
rightBack


angle = 90 degrees
axis = -1,0,0

(equivilant rotation to:
angle = -90 degrees
axis = 1,0,0)

  • c =cos(angle) = 0
  • s = sin(angle) = 1
  • t =1 - c = 1
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
1 0 0
0 0 1
0 -1 0

backLeft

angle = 120 degrees
axis = -0.5774,0.5774,0.5774

  • c =cos(angle) = 0.866
  • s = sin(angle) = -0.5
  • t =1 - c = 0.134
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 -1 0
0 0 1
-1 0 0

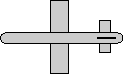
leftForward

angle = 180 degrees
axis = 0,0.7071,0.7071

  • c =cos(angle) = -1
  • s = sin(angle) = 0
  • t =1 - c = 2
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
-1 0 0
0 0 1
0 1 0

forwardRight

angle = 120 degrees
axis = -0.5774,-0.5774,-0.5774

  • c =cos(angle) = 0.866
  • s = sin(angle) = -0.5
  • t =1 - c = 0.134
[R] =
t*x*x + c t*x*y - z*s t*x*z + y*s
t*x*y + z*s t*y*y + c t*y*z - x*s
t*x*z - y*s t*y*z + x*s t*z*z + c
0 1 0
0 0 1
1 0 0
metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

cover us uk de jp fr caVisualizing Quaternions by Andrew J. Hanson

Other Math Books

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.