Maths - Continuity

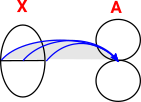
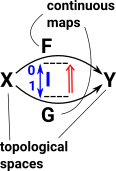Continuity Between Metric Spaces

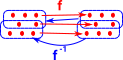
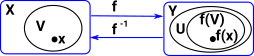
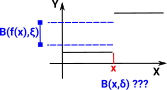
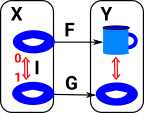
Even if we are mostly interested in continuity between non-metric spaces I think it helps intuition if we look at metric spaces first.

The diagram shows a function from X with a metric δ to Y with a metric ξ.

We have an open set which is a ball around x and an open set which is a ball around f(x).

For continuity, as the ball around x gets smaller we want the ball around f(x) to get smaller.

diagram
To visualise this as a function better lets draw these balls in two dimensions only: 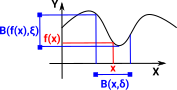diagram
As an example of a function that is not continuous lets take a function that has value 1 when x<3 and has value 4 when x<=3. 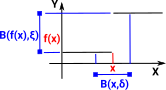diagram

Here we can see that there is a smaller ball (open set) in Y but it doesn't have a corresponding ball (open set) in X.

So we can start to see that there is a requirement, for continuity, that open sets in Y map through f-1 to open sets in X.

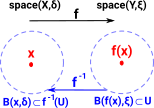
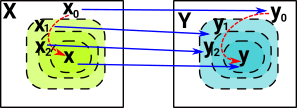
diagram

Continuous Maps

A function is continuous if it doesn't jump, that is, when two inputs of the function get close to each other then the corresponding outputs of the function get close to each other.

Here we discuss the most general form of continuous map which also applies to non-metric topological spaces.

A continuous mapping implies a limited kind of reversibility, at least locally.

Definition 1

Here is one definition of continuity, based on open sets:

Let X and Y be topological spaces. A function f : X->Y is continuous if f-1(V) is open for every open set V in Y. diagram

Definition 2

Another definition of continuity, based on neighbourhoods, is equivalent to the above definition.

Let X and Y be topological spaces. A function f : X->Y is continuous if for every x∈X and every open set U containing f(x), there exists a neighbourhood V of x such that f(V)containsU. continuity diagram

More detail about continuity on page here.

Continuous Surjective Maps

diagram

Here is an extreme case of a Surjective Map which maps to a single point.

This seems to meet the requirements as there is an open set round the whole preimage. We can think of surjections which meet these requirements as 'nice surjections'.

See fibrations

Continuous Injective Maps

diagram

Here is an extreme case of a Injective Map which maps from a single point.

In this case all the open sets in the codomain need to map back to a single open set in the domain. This meets the requirements so it is a 'nice injection'.

See cofibrations

Continuity as Pullback

This diagram shows a set of points being mapped to another set of points (in red).

For that map to be continuous the pre-image of every open set must be an open set (shown as blue map in the reverse direction).

diagram

Continuity and Limits

In the continuity between metric spaces examples at the top of this page we reduce the ball in the codomain and the ball in the domain must also reduce as the map is continuous.

The limit is when the ball in the codomain and the domain both reduce to a single point.

This idea of a limit generalises to continuous maps between non-metric topological spaces.

See page here about categorical limits.

Continuous Maps Preserve Limits

diagram

Topology Perspective

Let X and Y be topological spaces. A function f : X->Y is continuous if for every x∈X and every open set U containing f(x), there exists a neighbourhood V of x such that f(V)

Category Theory Perspective

The category Top has topological spaces as objects and continuous maps as morphisms.

The isomorphisms in this category correspond to homeomorphisms in topology.

Top preserves limits and co-limits. Simplicial sets are co-limits of Top.

Top is a category but it does not have exponential objects for all spaces and so it does not have some nice properties: it is not cartesian closed or a topos. If these properties are required then there may be variations of Top for the spaces required that have these properties. For example, nice topological spaces such as compactly generated topological spaces. Or see homotopy category at ncatlib.

See page here about categorical limits.

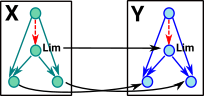diagram

Continuity of Maps between Lattice Structures

So far we have drawn diagrams with intersections and unions (Venn diagrams) but we could also draw these in terms of logic. 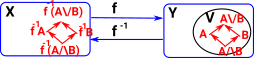diagram

Examples

In this diagram the points stay within their open sets. This is a continuous map, the pre-image of every open set is an open set. The intersections and unions of open sets play nicely together. 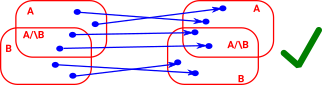diagram
This next example is not a continuous map because the preimage of A is not an open set because it includes A and A/\B but not B. We could think of this as a tear. 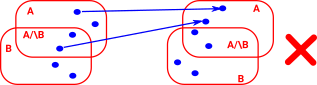diagram
Again this example is not a continuous map because the preimage of A is not an open set. 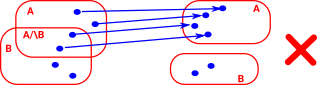diagram
In this example the whole space is shrunk to a point. This is a valid continuous map because the preimage A\/B is an open set. 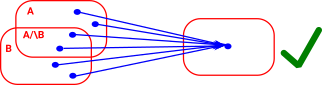diagram

Homotopy

diagram

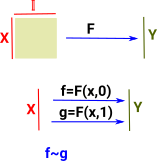
If we have two topological spaces X & Y with two continuous maps between them F & G then a homotopy is a continuous map between F & G.

In order to see how this is related to the map between the cup and torus I have drawn a map from a third shape (in this case another torus).

So as F continuously maps the G then the cup maps to the torus.

We can move the continuous map forward from the functions to the domain so the functions are homotopic if:

there existsH: X × [0,1] -> Y

where:

  • H(x,0) = F(x)
  • H(x,1) = G(x)

We can think of this as 'filling in' the gap between F and G so that we can take any path through it.

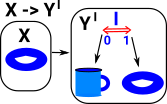 diagram
diagram Or we can draw it in the codomain (currying) so that each element in X maps to I->Y.

More about homotopy on page here.

diagram

Maps F & G are homotopic if:

there existsH: X × [0,1] -> Y

where:

  • H(x,0) = F(x)
  • H(x,1) = G(x)

We can think of this as 'filling in' the gap between F and G so that we can take any path through it.

There is a good video about this on a site here.

A homotopy is a function between functions with certain properties.

Let X and Y be topological spaces and f,g : X->Y be two continuous maps. Then f is said to be homotopic to g (written f~g) if there exists a map F : X×power set-> Y, called a homotopy such that F(x,0) = f(x) and F(x,1) = g(x) .

where:

  • f~g f is said to be homotopic to g
  • power setrepresents the unit interval [0,1]
  • continuity, in this context, is defined on page here
 homotopy

Fibrations and Continuous Maps

Some continuous maps between spaces have a 1:1 mapping between points, these continuous maps are known as homeomorphisms. It is also possible to have a continuous map from a line to a point, or vise versa, that is what we are discussing here.

diagram There is a continuous map from a line to a point. In the same way that in sets, attempting to reverse a surjective map leads to fibre bundles, with continous maps we get fibrations.
diagram This continuous map is reversible so we have a continuous map from a point to a line.
So, for example, two circles that touch at a point can be continuously deformed into a circle with a line through the middle. diagram

Or we can expand all the points on, say a circle, to get a band.

This is like a product of a circle and a line.

diagram

For more information see:

Transport

from here 
transport : Path U A B -> A -> B

That is, if we have a path from A to B and A, then B.

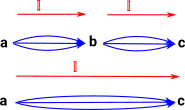
Composition of Paths

We want to compose these two paths:

  • p : Path A a b
  • q : Path A b c

from here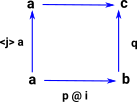

 
compPath (A : U) (a b c : A) (p : Path A a b) (q : Path A b c) : Path A a c =
   comp (<_> A) (p @ i)
                   [ (i = 0) ->  a
                   , (i = 1) -> q ]

Where 'comp' is a keyword with the following parameters:

  • a path in the universe.
  • the bottom of the cube we are computing.
  • a list of the sides of the cube

 

 

metadata block
see also:

Michael Robinson - Youtube from two-day short course on Applied Sheaf Theory:

  1. Lecture 1
  2. Lecture 2
  3. Lecture 3
  4. Lecture 4
  5. Lecture 5
  6. Lecture 6
  7. Lecture 7
  8. Lecture 8
Correspondence about this page

Book Shop - Further reading .

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

cover Introduction to Topological Manifolds (Graduate Texts in Mathematics S.)

Other Books about Curves and Surfaces

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2024 Martin John Baker - All rights reserved - privacy policy.