Maths - Ordered Sets

On these pages we are looking at set related categories. The category theory of a set is discussed on the page here. We then go on to look at sets with some additional structure. On this page we start to look at sets with an order relation added.

First lets look at this structure from a set theoretic point of view. That is we look inside the set, at its elements, rather than looking at its external category theoretic properties.

Strictly Ordered

First lets assume the relation is total and strictly ordered. That is for every pair of elements 'a' and 'b' then either: a<b or a>b.

Examples of strictly ordered sets are: The natural numbers. The natural numbers modulo n. strictly ordered sets are: transitive: if a<b and b<c then a<c But they don't have the following properties: reflexive: not a<a symmetric: not if a<b then b<a

If S is a set, then the order relation on S can be considered as a subset of S×S or a map S×S-> π where π is the truth object (in this case Boolean).

More about order relation on page here

So how is the category defined?

Objects The objects are {}, {0}, {0,1}, {0,1,2}, {0,1,2,3} and so on. Not necessarily labeled but it helps understanding to label with numerals. As with general sets the objects are a 0 element set, a 1 element set, a 2 element set and so on but here

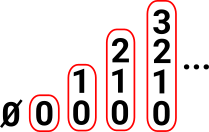Arrows Arrows are order preseving functors (or cofunctors - see below) between these objects. That is: if a<b then F a < F b

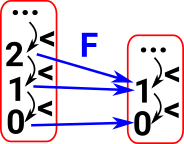Weakly Ordered

Here the relation is total and strictly ordered. That is for every pair of elements 'a' and 'b' then then it could be that: a<=b or a>=b or both a=b.

Weakly ordered sets are: reflexive: a<=a transitive: if a<=b and b<=c then a<=c But they don't have the following properties: symmetric: not if a<=b then b<=a Although for some cases its possible that a<=b and b<=a.

If S is a set, then the order relation on S can be considered as a subset of S×S or a map S×S-> π where π is the truth object (in this case Boolean).

More about order relation on page here

So how is the category defined?

Objects Not necessarily labeled but it helps understanding to label with numerals. As with general sets the objects are a 0 element set, a 1 element set, a 2 element set and so on but here the objects are {}, {0}, {0,1}, {0,1,2}, {0,1,2,3} and so on. Also objects where the elements are repeated such as {0,0}, {0,0,1}, {0,1,1} and so on. These are known as degenerate sets.
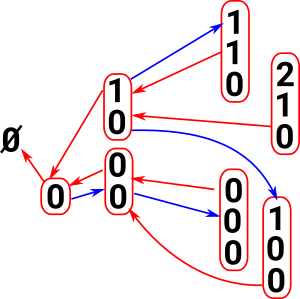Arrows The arrows preserve this weak order. That is: if a<=b then F a <= F b

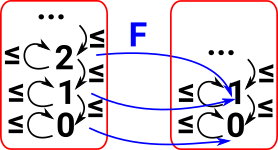Decomposing Arrows

Order preserving arrows can be decomposed into a sequence of arrows that insert or merge single elements one at a time.

We will call these elemental mappings di and si di is an injective mapping which goes from a set of size n to a set of size n+1 si is a surjective mapping which goes from a set of size n to a set of size n-1

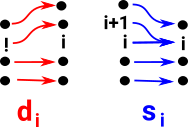
So we can construct any order preserving mapping from a sequence of d_i and s_i.

Decomposing Arrows in Set^op

Set^op is a category with the same objects as set but where the arrows are reversed as explained on the page here. In this case order preserving arrows can again be decomposed into a sequence of arrows although , in this case, we don't have the concept of injective and surjective mappings (or we have the reverse of these concepts).

So the elemental mappings di and si become: face map: di is a mapping (reverse of injective) which removes element 'i' and goes from a set of size n to a set of size n-1. degeneracy map: si is a mapping (reverse of surjective) which duplicates an element and goes from a set of size n to a set of size n+1

Subobjects

We can create any subobject using a sequence of face maps.

Equalities

Degeneracy maps create equal elements.

Identities

Note: when combining maps below the map on the right is done first. For example, d_i d_j means d_i after d_j (do d_j then do d_i).

Identity	diagram
di dj = dj-1 di if i < j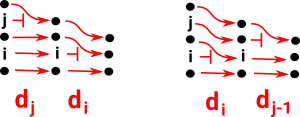
di sj = s j-1 di if i < j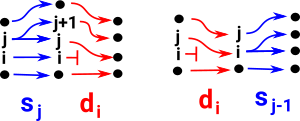
dj sj = id = dj+1 sj
di sj = sj di-1 if i > j+1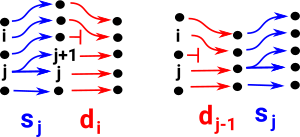
si sj = s j+1 s i if i ≤ j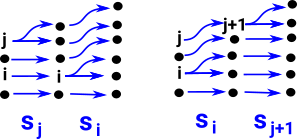

Simplicial Sets

See page here about simplicial sets.

EuclideanSpace

home

Prerequisites

This page looks at sets from a category theory point of view. For a set theory view see page here.

For an introduction to category theory see page here.

To expand this topic further see Topos Theory.

Books

Sets for Mathematics - This is a book about sets from category theory point of view.