Weak equivilance provides a simpler way to determine equivilance.
| On the equivilance page we discussed how to determine equivilance by finding two functors. F and G, which give the identity when composed in both directions. |  |
 |
|
| Weak equivilance gives us a way to do this using only a functor in one direction F. However this only tells us that an equivilance exists, not the functors which give the equivilance. |  |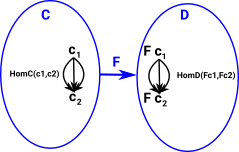
Given this functor F : C -> D there is an equivalence if and only if the following are all true:
- F is full, i.e. for any two objects c1 and c2 of C, the map HomC(c1,c2) -> HomD(Fc1,Fc2) induced by F is surjective;
- F is faithful, i.e. for any two objects c1 and c2 of C, the map HomC(c1,c2) -> HomD(Fc1,Fc2) induced by F is injective; and
- F is essentially surjective (dense), i.e. each object d in D is isomorphic to an object of the form Fc, for c in C.
More about topology related categories on page here.
Weak Factorisation System
Example in SetIn a set category where morphisms are functions. Each function can be factored into injective and surjective (epi and monic) functions. Or we can look at this as fibre and co-fibre. More about fibres on page here. |
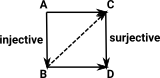 The square commutes, the function from A to D factors so there must be a unique arrow (shown dotted) to connect them. |
|
Example in Simplical SetHere all functions are (weakly) order preserving. These can be factored into degenerate arrows (which increase dimension) and arrows which remove a dimension. More about simplical sets on page here. |
Further Information
Weak equivalence was first used in algebraic topology, in particular, in model category theory as described on the page here.