Here we look at a two dimensional euclidean space embedded in a three dimensional projective space, we are using the hemisphere model to do this projection.
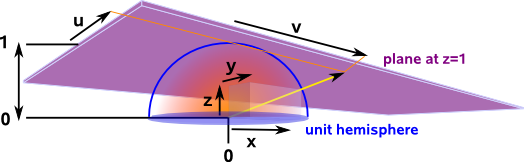
In two dimensional projective space using hemisphere model:
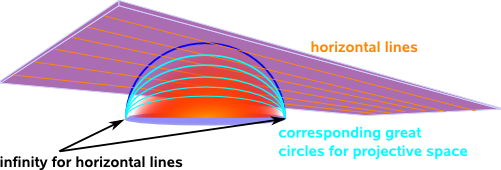
- Straight lines in euclidean space map to great circles (or semi circles) in projective space.
- Horizontal lines meet at (±1,0,0) which is the point at infinity for horizontal lines.
- Vertical lines meet at (0,±1,0) which is the point at infinity for vertical lines.
- The line at infinity is the line around the sphere at z=0, a point on this line represents direction.
From the above we can see that, as we move away from the origin, lines that cross at 90° in euclidean space do not cross at 90° in projective space. So angles away from the origin are not conserved by the projection.

Derivation for translation between projective (hemisphere) and euclidean spaces
Since we are projecting using a straight line then there is a linear relationship between a point on the plane and its projection on the sphere:
|
= λ |
|
where:
- (x,y,z) = projective coordinates
- (u,v) = euclidean coordinates
- λ = expansion factor of vector: function of (x,y,z) or (u,v)
Dividing the top two rows by the bottom row gives the euclidean coodinates in terms of the projective coordinates:
|
= |
|
To go the other way from the projective coordinates to the euclidean coodinates we need to use the information that the coordinates are constrained to a unit sphere so:
x² + y² + z² = 1
rearanging gives:
x²/z² + y²/z² + 1 = 1/z²
u² + v² + 1 = 1/λ²
λ = ±1/√(u² + v² + 1)
substituting this into the first vector equation gives:
|
= ±1/√(u² + v² + 1) |
|

