Even when we are dealing with spaces with many dimensions there is still a scalar quantity that defines many of the properties of that space; that property is the distance function.
We need the idea of distance before we can define many of the fundamental constructs of geometry such as a 'straight line' although there are other constructs like 'angle' and 'shape' that don't depend on distance.
The distance function, given two points P1 and P2, will give us a scalar quantity: representing the 'distance' between P1 and P2.
We have said that the distance is a scalar quantity but there are some geometries, such as Minkowski space, where the distance value may be either real or imaginary (square root of a negative number).
Properties of the distance function
It does not add.
That is if P1 is D1 from P2 and P2 is D2 from P3 it is not necessarily true that P1 is D1+D2 from P3 (unless P1,P2 and P3 are on a straight line)

It is independent of the origin and orientation of the coordinate system.
For instance if we measure the distance between P1 and P2 (using distance=√((P2.x-P1.x)²+(P2.y-P1.y)²)) we will get a value:
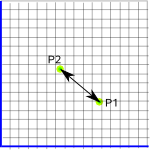
If we then change the origin and orientation of the coordinate system, the coordinates of P1 and P2 will change but the distance between them will not change.
Although it does depend on the units of the coordinate system.
Meaning of Zero Distance.
In Euclidean space, if the 'distance' between two points is zero then the points are identical (have the same coordinates) but in other geometries such as Minkowski geometry this is not necessarily true. This case is called a pseudo-metric.
The metric defines how we measure distances between points.
We can plot points using some coordinate system but this does not necessarily tell us a lot about the underlying geometry because we are free to choose any origin or orientation or coordinate system such as cartesian, polar, cylindrical, etc. What we need is a measure that is independent of such arbitrary choices. A possible measure is 'distance', once we have a measure of distance we can then define a straight line and other geometrical constructs.
In Euclidean Space

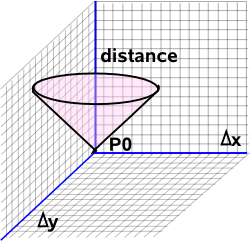
If we start with Euclidean space then the distance from P0 is:
Δs = √(Δx²+Δy²+Δz²)
If we take the two dimensional case and plot the distance form P0 in the third dimension we will get a cone like this:
In Other Spaces
Δx²= -ve and Δy²= -ve
What if we choose a different space, for instance, what would be the metric of a two dimensional space where both dimensions square to negative? We will assume the same equation for the metric:
Δs = √(Δx²+Δy²)
Since Δx and Δy both square to -ve, then Δs = √-ve, so the distance dimension is also 'imaginary' (squares to -ve). Since the distance function is expected to be a real number we could redefine the metric as follows:
Δs = √(-Δx²-Δy²)
so that it gives a real number distance.
Δx²= +ve and Δy²= -ve
If we have a mixture of dimensions, some of which square to to positive and some square to negative, then the situation gets more complicated. Lets start with the situation where the x dimension squares to +ve, the y dimension squares to -ve, and we will add a third dimension to show the distance from the origin. Like the above cases the result is a cone, this time 2 cones, split and rotated through 90°. as shown here:
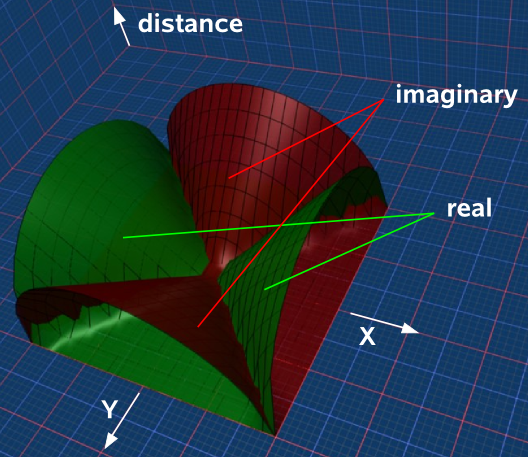
So now we will try mixed dimensions say Δx²= positive and Δy²= negative. To make this a bit simpler lets first plot the distance squared:
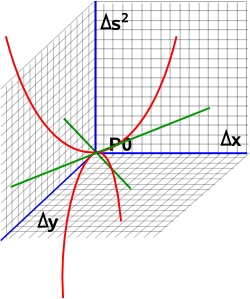
So if we plot along the x axis (top red line) we always get a positive result and if we plot along the y axis (bottom red line) we always get a negative result. If we plot along lines which are 45° to Δx and Δy (green lines) then the distance function is zero.
So the metric Δs = √(Δx²-Δy²) will be a complex number with real and imaginary parts but solutions with imaginary parts, in Minkowski space, represent cases of traveling faster than light.
Δx²= 0 and Δy²= 0
What if we choose a different space, for instance, what would be the metric of a two dimensional space where both dimensions square to zero?
These are known as null vectors, but what does this mean? Using this metric, points along these lines are zero distance from P0, so are these points all effectively the same point? If we add two more 'space' dimensions to make Minkowski space then these are the lines that light travels along. We have to be careful about treating these points as zero distance apart, for instance: if we have 3 points P0, P1 and P2 and if P1 is zero distance from P0 and P2 is zero distance from P0 this does not necessarily mean that P1 is zero distance from P2.
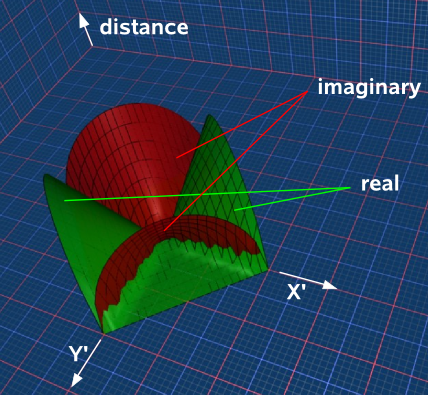
Properties of Distance
How can we:
- Combine distances?
- Find the shortest distance?
- Use distance to define a straight line?
If we take the case of Euclidean space then, if we go from A to B via C,
- If distance A,B = distance A,C + distance C,B then C lies on the shortest distance (defined as a straight line) between A and B.
- If distance A,B < distance A,C + distance C,B then C lies outside the shortest distance between A and B.
- Distance A,B cannot be > distance A,C + distance C,B because if it were it would not be the shortest distance.
But what about a space where Δx²= positive and Δy²= negative, how do we define the shortest distance then? This space is more complicated, for instance, if we take two points 'A' and 'B' which are zero distance from the origin (because they are on 45° diagonals) they are not zero distance from each other. So how do we define the shortest distance (straight line) between A and B?
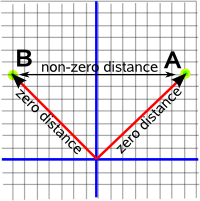
So it would seem that the shortest distance between 'A' and 'B' ? it would seem that the shortest distance is zero if we go via the origin? But if we allow this then the shortest distance between any two points is zero because we can always zigzag along diagonals (like the bishop in chess).
So these must be something else we need to consider when working out the shortest distance in such a space. We will return to this theme when we discuss Minowski space on this page.
