There are cases where we want to treat points at infinity like any other points. For instance we might want to:
- Treat parallel lines like other lines and find the point where they meet.
- Treat translations as a rotation about infinity.
So how can we do this? One first thought might be to map an infinite line onto a finite line like this:
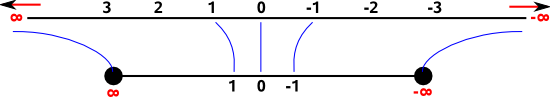
So the top line is an infinite line as we usually imagine it, disappearing off the page infinitely in each direction. We want to map this to a finite line, with infinity shown as actual points on the line, like the line below it. This is going to have to be a non-linear mapping because we still want finite distances, like the distance between 0 and 1, to appear as finite distances on our new line so the representation of a unit interval is going to get less and less as we approach infinity.
It may appear that we are loosing information by doing this mapping, but this is not necessarily so, the blue lines show that each point on one of the lines is mapped in a 1:1 way to a corresponding point on the other line.
So what function could we use for such a mapping? It would have to diverge very sharply as the numbers got bigger; even more than an exponential function.
Stereographic Projection
One possible answer to this is to extend the finite line to a second dimension. We can then represent the finite line as a semicircle:
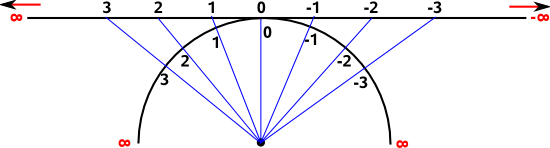
The mapping depends on the distance between the centre of the circle and the line, to keep things simple we will choose a distance of 1. This is linear in two dimensions, in that the projection is done by a straight line, although it is not linear in the sense that equal distances in the straight line are not equal distances on the semicircle.
So the one dimensional function is the inverse tangent: atan.
| infinite line | finite line semicircle |
angle |
||
|---|---|---|---|---|
| x | y | x'=x/√(x²+1) | y'=1/√(x²+1) | atan(x) |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0.78 | ||
| 2 | 1 | 1.11 | ||
| 3 | 1 | 1.25 | ||
| ∞ | 1 | 1 | 0 | 1.57 |
It may be a problem that we are only using half of the circle, it is usually considered that opposite points on the circle represent the same point.
There is an alternative projection, without this issue of each point being represented as two points on the circle, this projects the point from the opposite side of the circle.
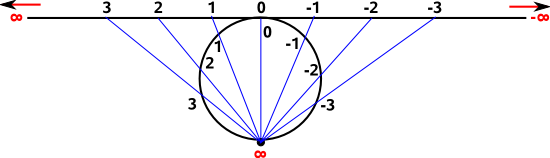
Let:
- x and y be coordinates along the line.
- x' and y' be coordinates along the circle.
since they are connected by a straight line then:
|
= λ |
|
where λ is a constant.
being a line and a circle also imposes the following constraints:
y=1 for the line
x'² +(y'-0.5)² = 0.5² for the circle
expanding out the last equation gives:
x'² = 0.5² - (y'-0.5)² = 0.25 - (y'² -y' +0.25) = y'² -y'
from the λ equation we get:
x/y = x'/y'
substituting the equations for the line and circle into this gives:
x = x'/y' = √(y'(y' - 1))/y' = √(y'(y' - 1)/y'²) = √(1 - 1/y')
Möbius Transform
We can represent this mapping with a Möbius transform (described here) which maps a complex plane 'z' to another complex plane 'w' as follows:
![]()
where a,b,c and d are complex constants.
If we start with a simple case where a=d=0 and b=c=1 so:
w=1/z
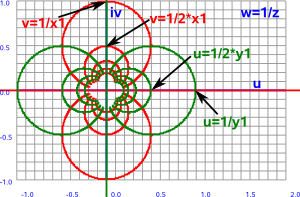
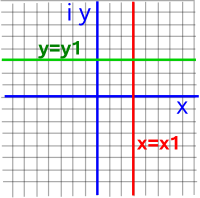
This inverse function is described on this page, we can see that vertical (red) and horizontal (green) lines in the z plane map to circles in the w plane:
| z plane | w plane | |
|---|---|---|
 |
--> w=1/z |
|
The whole line in the z plane (including the point at infinity) is therefore mapped to the circle. The point at ∞ in z is mapped to 0 in the w plane. As long as the line does not go through the origin, in which case it would map to another line (infinite diameter circle), then we do not need to be concerned what the point (0,0) maps to.
Higher Dimensions
Möbius transforms as defined in terms of complex numbers so we can map between a 1D Euclidean space to a 2D spherical space.
Can this be extended to 'n' dimensions in some way?
How do we represent higher dimensional stereographic projections?
What are 'linear fractional transforms' ?
What are 'complex projective space' and 'quaternionic projective space'.