Abstract
On this page we look at spherical and elliptic geometry.
As an example of spherical geometry we will look at a two dimensional algebra although such geometries can occur in different numbers of dimensions.
In two dimensions we can represent this geometry as the surface of a 3D sphere, that is, we can embed an 'n' dimensional non-euclidean space in an 'n+1' dimensional euclidean space.
We start with a traditional approach based on postulates.
We then go on to look at the 1:1 equivalence (a morphism) between the rotation of a 3D rigid body and the movement of a shape on the surface of a sphere
Spherical and Elliptic Geometry
In both cases space curves inward so all lines meet. In spherical geometry lines meet twice at the antinodal points and in elliptic geometry lines meet only once.
Spherical Geometry
A 'straight' line represents the shortest distance between two points P1 and P2:
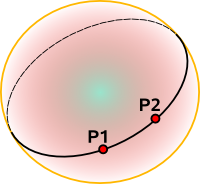
The line can also continue around the back of the sphere, this part of the line being the longest distance between the points. So a straight line goes all the way around the sphere with a length of 2πr.
Although we are currently visualising the sphere as an surface in 3 dimensional Euclidean space it is actually a 2 dimensional non-euclidean space.
Any two lines intersect twice, these intersections are known as antinodal points and are on opposite sides of the sphere.
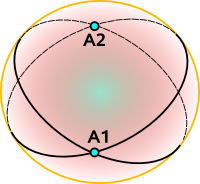
Elliptic geometry
In elliptic geometry any two lines intersect once.
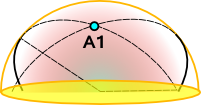
Spherical Geometry and 3D Rotation
There is a 1:1 equivalence (a morphism) between the rotation of a 3D rigid body and the movement of a shape on the surface of a sphere. Note that this is a shape rather than a point because we need to be able to specify a rotation θ in the spherical plane in addition to Latitude and Longitude. This gives us three degrees of freedom as with solid body rotation.
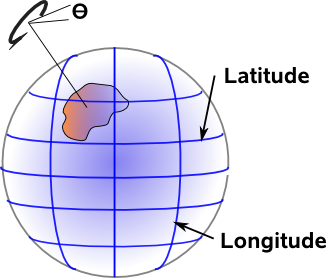
Perhaps a better way to look at this is to let the solid body be the sphere itself, then the surface of the sphere is automatically the same as rotation in 3D space. This equivalence seems almost trivial but if we can map the surface of the sphere to euclidean space then we can derive a model for isometries.
This is discussed on the projective and conformal space pages.
