Maths - Hyperbolic Geometry

In Rienmannian geometry space can curve at different places (see manifolds) here we look at geometries where the curve of space is constant.

Eulidean Geometry flat space
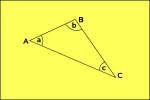Hyperbolic Geometry space curves outward
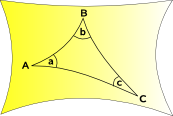Spherical Geometry and Elliptic Geometry space curves inward

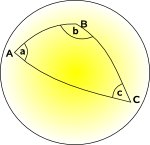Terminology

Here we look at the terminology such as geometries, spaces, models, projections and transforms. Its quite difficult when we start dealing with non-Euclidean geometries because we use similar terminology that we are used to in conventional Euclidean space but the terms can have slightly different properties. For example, the concept of a 'line' can look different in different geometries:

Geometries and Spaces

Rienmannian geometry defines spaces generally in terms of manifolds, here we are interested in homogeneous, isotropic spaces which have no preferred points or directions, examples are:

	parallel postulate - number of unique parallel lines through point	space curves	Inventors	Point at Infinity	Distance Measure
Eulidean Geometry	1	none	Euclid	where parallel lines meet	√(x² + y²)
Hyperbolic Geometry	∞	space curves outward so lines dont meet	Lobachevskii and Bolyai
Spherical Geometry Elliptic Geometry	0	space curves inward so all lines meet

 

Models

Examples are:

• Upper half-plane model
• Poincare disc model
• Projective model
• Conformal model

Projections

Stereographic Projection

Transforms

Invariant

Examples are:

• Möbius Transform
• Lorentz Transform

 

Parallel Postulate

If we take away the parallel postulate from Euclidean Space.

This leads to:

• parallel postulate is false
• the angles of a triangle do not add to π
• for a shape of a given size, there does not in general, exist a similar shape of a larger size.

Possible mappings between Euclidean Space and Hyperbolic Space:

• projective
• conformal

properties:

	projective	conformal (Poincaré disc )
straight lines - geodesics		segments of circles
angle		preserved
internal angles of triangle		π-(α+β+γ)=CΔ
distance between two points		ln

 

EuclideanSpace

home

Prerequisites

This page uses general geometry concepts such as coordinates and trigonometry.

It is also useful to understand the concept of manifolds.

Since we will project these spaces onto the complex number plane we need to know about complex numbers.

Hyperbola

Minkowski Metric

Lie Group