Maths - Combined Rotation and Translation

Prerequisites

How can we combine rotations and translations without using matrices?

If you are not familiar with this subject you may like to look at the following pages first:

• Rotations

Combined Rotation and Translation

In VRML and related standards there is the concept of a transform group. This is a node in a scenegraph which contains the following parameters:

center="0 0 0"
rotation="0 0 1 0"
scale="1 1 1"
scaleOrientation="0 0 1 0"
translation="0 0 0"

To simplify things at this stage assume that the node contains only:

center="0 0 0"
rotation="0 0 1 0"
translation="0 0 0"

Rotation about a Point

Here we cover the rotation about a point (not necessarily the origin). This can be solved using matrix methods as shown here.

First as a comparison consider a rotation about the origin.

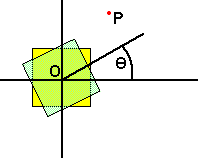
• Angle = theta
• translation = 0

Now imagine the same object being rotated by the same angle, but about point P.

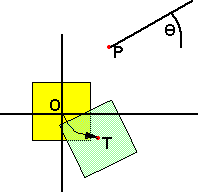
• angle = theta
• translation = T = C - rotate(C)

Where:

• T = translation caused by the rotation.
• C = the point we are rotating about.
• R(C) = the rotate function applied to point C

So the angle of rotation is the same whatever point we rotate about, but if we rotate about a point other than the origin this will translate the centre of the object by C - R(C).

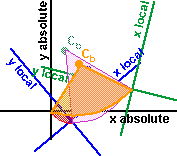
Rotating Sum of two points

What is the effect of applying the rotation function R() to the sum of two points?

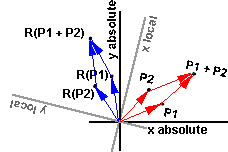
What this diagram is trying to show (I realise that the diagram is a bit messy) is that if:

Point P1, in absolute coordinates, is rotated to point R(P1) in local coordinates.

Point P2, in absolute coordinates, is rotated to point R(P2) in local coordinates.

Then:

Point P1+P2, in absolute coordinates, is rotated to point R(P1+P2) in local coordinates.

So:

R(P1+P2) = R(P1) + R(P2)

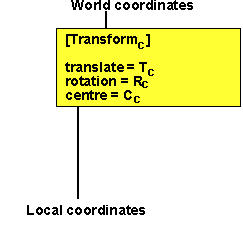
Transforms

Let us take a transform with the following parameters:

• T = translation
• R() = rotation function
• C = centre of rotation

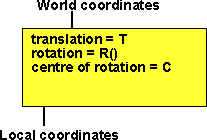
To calculate the total transform in terms of these parameters, we need to first shift the centre of rotation to the origin, then rotate, then shift back to the original centre.

So first shift C to origin: Pabsolute = Plocal - C
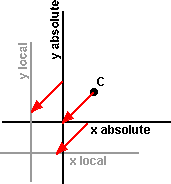Now rotate about origin: Pabsolute = R(Plocal - C)
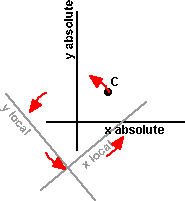Now move back to original point: Pabsolute = R(Plocal - C) + C

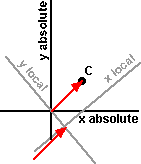Now add the translation:

P_absolute = R(P_local - C) + C + T

The terms in the rotation function can be spilt up as described in 'Rotating Sum of two points' above.

P_absolute = R(P_local) - R(C) + C + T

Combining Transform Nodes

What is the combined effect of putting one transform node under another:

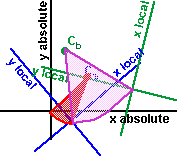It is possible to find the resulting transform in terms of a 4x4 matrix. But what is an equivalent Transform node that will have the same effect as the two nodes above:

For on level of transform we have seen that the absolute position is given by:

P_absolute = R(P_local - C) + C + T

To cascade more than one of these we can calculate the position in coordinates of layer 'n' from the position in the coordinates of the layer below:

P_n-1 = R_n(P_n - C_n) + C_n + T_n

where:

• P_n = position of point in coordinates of layer n
• R_n = rotation function of layer n in coordinates of layer n-1
• P_n-1 = position of point in coordinates of the layer below n
• C_n = centre of rotation of layer n in coordinates of layer n-1
• T_n = translation on layer n in coordinates of layer n-1

So P_absolute = R_a(P_a - C_a) + C_a + T_a
and P_a = R_b(P_b - C_b) + C_b + T_b

where:

• R_a = rotation function of transform a in absolute coordinates
• C_a = centre of rotation of transform a in absolute coordinates
• T_a = translation of transform a in absolute coordinates
• R_b = rotation function of transform b in coordinates of transform a
• C_b = centre of rotation of transform b in coordinates of transform a
• T_b = translation of transform b in coordinates of transform a

So substituting the Pa from the second equation into the first gives:

P_absolute =R_a(R_b(P_b - C_b) + C_b + T_b - C_a) + C_a + T_a

Expanding out gives:

P_absolute =R_a R_b(P_b - C_b) +R_a (C_b + T_b - C_a) + C_a + T_a

We want to put this into this format:

P_absolute = R_t(P_b - C_t) + C_t + T_t

where:

• P_absolute = position of point in absolute coordinates
• R_t = equivalent total rotation
• P_b = position of point in coordinates of transform b
• C_t = centre of equivalent total rotation
• T_t = equivalent total translation

so to make this equivalent to the two separate rotations makes:

• R_t = equivalent total rotation = R_a R_b
• C_t = centre of equivalent total rotation = C_b
• T_t = equivalent total translation = R_a (C_b + T_b - C_a) + C_a + T_a - C_b

So we rotate around a point which is equal to the centre of rotation of the first level rotation, but we have to adjust the translation by a factor which depends on the absolute rotation.

Example 1

Imagine that we are implementing a trackerball control. To do this we are translating an object in a transform under another transform, the lowest level transform rotates everything by 45 degrees. We pull the object across the screen and we want it to move across the screen but how do we correct for the bottom transform.

We are setting the lowest level transform:	but we want it to be equivalent to the following
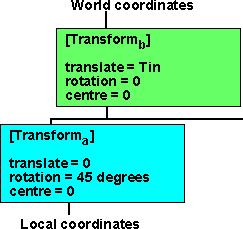equivalent total translation = Ra (Tb)	equivalent total translation = Tin

Therefore Tb = Ra'(Tin)

In other words we apply the inverse rotation to the input translation which is minus 45degrees.

Example 2

As example 1 but with translation and off-centre..

We are setting the lowest level transform:	but we want it to be equivalent to the following
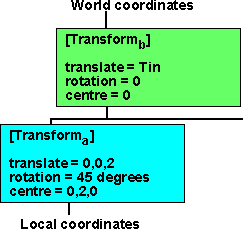equivalent total translation = Ra (Tb - Ca) + Ca + Ta	equivalent total translation = Ta + Tin

Therefore R_a (T_b - C_a) + C_a + T_a = T_a + T_in

R_a (T_b - C_a) + C_a = T_in

T_b = R_a'(T_in - C_a) + C_a

Scaling, Translation and Rotation.

We now want to add scaling to the following parameters:

• T = translation
• R() = rotation function
• C = centre of rotation

We add the following two parameters:

• The S (scale) field specifies a non-uniform scale of the coordinate system. Scale values shall be greater than zero.
• The SR (scaleOrientation) specifies a rotation of the coordinate system before the scale (to specify scales in arbitrary orientations). The scaleOrientation applies only to the scale operation.

The position in terms of local position is:

P_absolute = R(SR(S × SR'(P_local-C))) + T + C

Combining Transform Nodes with Scale

What is the combined effect of putting one transform node under another:

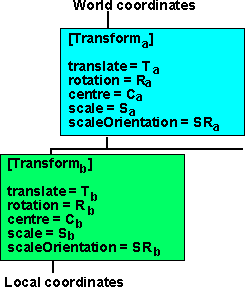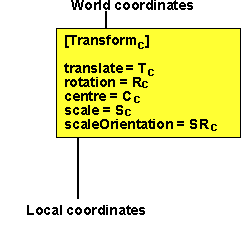For on level of transform we have seen that the absolute position is given by:

P_absolute = R(SR(S × SR'(P_local-C))) + T + C

To cascade more than one of these we can calculate the position in coordinates of layer 'n' from the position in the coordinates of the layer below:

P_n-1 = R_n(SR_n(S_n × SR_n'(P_n-C_n))) + T_n + C_n

where:

• P_n = position of point in coordinates of layer n
• R_n = rotation function of layer n in coordinates of layer n-1
• P_n-1 = position of point in coordinates of the layer below n
• C_n = centre of rotation of layer n in coordinates of layer n-1
• T_n = translation on layer n in coordinates of layer n-1
• S_n = scale of layer n in coordinates of layer n-1
• SR_n = scale rotation function of layer n in coordinates of layer n-1

So P_absolute = R_a(SR_a(S_a × SR_a'(P_a-C_a))) + T_a + C_a
and P_a = R_b(SR_b(S_b × SR_b'(P_b-C_b))) + T_b + C_b

where:

• R_a = rotation function of transform a in absolute coordinates
• C_a = centre of rotation of transform a in absolute coordinates
• T_a = translation of transform a in absolute coordinates
• S_a = scale of transform a in coordinates of layer n-1
• SR_a = scale rotation function of transform a in coordinates of layer n-1
• R_b = rotation function of transform b in coordinates of transform a
• C_b = centre of rotation of transform b in coordinates of transform a
• T_b = translation of transform b in coordinates of transform a
• S_b = scale of transform b in coordinates of layer n-1
• SR_b = scale rotation function of transform b in coordinates of layer n-1

So substituting the Pa from the second equation into the first gives:

P_absolute =R_a(SR_a(S_a × SR_a'((R_b(SR_b(S_b × SR_b'(P_b-C_b))) + T_b + C_b)-C_a))) + T_a + C_a

Can anyone help me expand this out and find an equivilant single transform??

Further Reading

You may be interested in other means to represent orientation and rotational quantities such as:

• Axis and Angle
• Quaternions
• Matricies

Or you may be interested in how these quantities are used to simulate physical objects:

• Kinematics

EuclideanSpace

home

Matrix vs. Quaternion

Car Racing Game

Transforms

Successive Rotations