3D Modelling - Martin Baker

3D Theory - Transform Group

Prerequisites

How to combine rotations and translations is scenegraph shown here:

Transform Group

Order of transforms

In addition to the translation and rotation, described here, the Transform group also allows a (possibly) non-uniform scale about an arbitrary point.

To do these 3 things we have the following parameter:

The T (translation) field specifies a translation to the coordinate system.
The R (rotation) field specifies a rotation of the coordinate system.
The C (centre) field specifies a translation offset from the origin of the local coordinate system (0,0,0).
The S (scale) field specifies a non-uniform scale of the coordinate system. Scale values shall be greater than zero.
The SR (scaleOrientation) specifies a rotation of the coordinate system before the scale (to specify scales in arbitrary orientations). The scaleOrientation applies only to the scale operation.

Given a 3-dimensional point P and Transform node, P is transformed into point P' in its parent's coordinate system by a series of intermediate transformations. In matrix transformation notation.

P' = T × C × R × SR × S × -SR × -C × P
The following Transform node:

Transform {
centre C
rotation R
scale S
scaleOrientation SR
translation T
children [...]
}
is equivalent to the nested sequence of:

Transform {
	translation T 
	children Transform {
		translation C
		children Transform {
			rotation R
			children Transform {
				rotation SR 
				children Transform {
					scale S 
					children Transform {
						rotation -SR 
						children Transform {
							translation -C
							children [...]
						}
					}
				}
			}
		}
	}
}

Code

public void calcTransform(sfvec3f translation, sfrotation rotation, sfvec3f center, sfvec3f sc, sfrotation scaleOrientation){
   setIdentity();
   if (translation != null) translate(translation);
   if (rotation != null) rotate(rotation,center);
   if (scaleOrientation != null) rotate(scaleOrientation,center);
   if (sc != null) { // if scale is (0,0,0), such as when scale first
   // enabled this will generate a non-afine error
   // so do following check
   if ((sc.x != 0) & (sc.y != 0) & (sc.z != 0)) scale(sc);
   if (scaleOrientation != null) rotate(scaleOrientation.minus(),center);
}

Example: To implement a trackball control

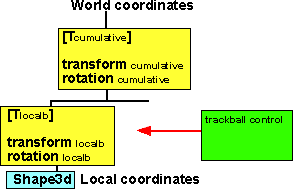
Assume we have a shape in a scenegraph under one or more Transform Groups, we want a trackball control to apply rotation to the Transform adjacent to the Shape3D node. The problem is that the cumulative rotations above it will modify it, so when we move the mouse right we want the object to rotate about the y-axis but the cumulative rotation will effect this and cause it to rotate about some other axis.

What we want is the equivalent of the following where a transform is added at the root of the tree, this will ensure that moving the mouse right will make the object to rotate about the y-axis.

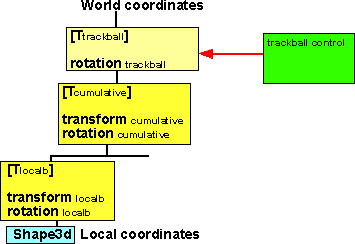
The problem with this solution is that any other shapes in the scenegraph will also be transformed. What we want to work out is an equivalent rotation in the local Transform which will have the same effect as this.

So in the required rotation is:

[Rcumulative] * [Rlocal]

where:

[Rlocal] = the new local rotation after the tracker ball is applied.
[Rcumulative] = the total effect of all the rotations in the tree excluding the local transform.
in other words Rcumulative is applied first, then multiplied by Rlocal

We want this to be equivalent to:

[trackball] * [Rcumulative] * [Rlocalb]

where:

[Rlocalb] = the local rotation before the tracker ball is applied
[Rcumulative] = the total effect of all the rotations in the tree excluding the local transform.
[trackball] = the rotation applied by the trackerball.
In other words apply trackball then multiply by Rcumulative then multiply by Rlocalb

Since we want these to be equivalent then:

[Rcumulative] * [Rlocal] = [trackball] * [Rcumulative] * [Rlocalb]

so if we pre-multiply both sides by the conjugate of Rcumulative we get:

[Rcumulative]' * [Rcumulative] * [Rlocal] = [Rcumulative]' * [trackball] * [Rcumulative] * [Rlocalb]

cancelling out [Rcumulative]' * [Rcumulative] gives

[Rlocal] = [Rcumulative]' * [trackball] * [Rcumulative] * [Rlocalb]

metadata block

see also:	Using scenegraph to model Physics Graph Theory
Correspondence about this page

3D Theory - Transform Group

Prerequisites

Order of transforms

Code

Example: To implement a trackball control

Further Reading

EuclideanSpace