Maths - Calculation of Matrix for 3D Rotation about a point

Abstract

On this page we will show that a rotation, about any point, is equivalent to a rotation (by the same angles) about the origin combined with a linear translation. We already have lots of methods for calculating a rotation about the origin (such as matrices and quaternions) so to rotate about any point, other than the origin, we do the rotation as if it was around the origin then apply a linear transform to get the same result.

This applies to both two and three dimensional transforms.

We will then go on to show that, in two dimensions only, that the converse is also true. That is any combination of translation and rotation can be represented by a single rotation provided that we choose the correct point to rotate it around.

Prerequisites

If you are not familiar with this subject you may like to look at the following pages first:

• Affine Transformation
• Matrices
• Rotations

Combined Rotation and Translation

In order to calculate the rotation about any arbitrary point we need to calculate its new rotation and translation. In other words rotation about a point is an 'proper' isometry transformation' which means that it has a linear and a rotational component.

Assume we have a matrix [R0] which defines a rotation about the origin:

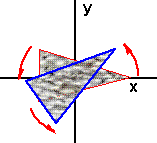
We now want to apply this same rotation but about an arbitrary point P:

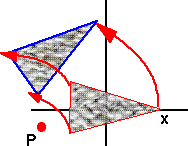
As we can see its orientation is the same as if it had been rotated about the origin, but it has been translated to a different point on space by the rotation.

In order to prove this and to calculate the amount of linear translation we need to replace:

• translate about arbitrary point P (Px,Py,Pz).

With the following 3 simpler transforms which, when done in order, are equivalent:

• translate the arbitrary point to the origin (subtract P which is translate by -Px,-Py,-Pz)
• rotate about the origin (can use 3x3 matrix R0)
• then translate back. (add P which is translate by +Px,+Py,+Pz)

So if we are using the global frame-of-reference (as explained here) then,

[resulting transform] = [third transform] * [second transform] * [first rotation]

[resulting transform] = [+Px,+Py,+Pz] * [rotation] * [-Px,-Py,-Pz]

Note for matrix algebra, the order of operations is important, so these translations do not cancel out.

So matrix representing rotation about a given point is:

[R] = [T]^-1 * [R0] * [T]

where:

[T]^-1 = inverse transform = translation of point to origin

1	0	0	x
0	1	0	y
0	0	1	z
0	0	0	1

[R0] = rotation about origin (if this is not clear see this discussion)

r00	r01	r02	0
r10	r11	r12	0
r20	r21	r22	0
0	0	0	1

[T] = translation of origin to point

1	0	0	-x
0	1	0	-y
0	0	1	-z
0	0	0	1

 

when these matrices are multiplied this will give the following result for rotation about x,y:

1 0 0 x 0 1 0 y 0 0 1 z 0 0 0 1

*

r00 r01 r02 0 r10 r11 r12 0 r20 r21 r22 0 0 0 0 1

*

1 0 0 -x 0 1 0 -y 0 0 1 -z 0 0 0 1

 

1 0 0 x 0 1 0 y 0 0 1 z 0 0 0 1

*

r00 r01 r02 -r00*x - r01*y - r02*z r10 r11 r12 -r10*x - r11*y - r12*z r20 r21 r22 -r20*x - r21*y - r22*z 0 0 0 1

 

r00	r01	r02	x - r00*x - r01*y - r02*z
r10	r11	r12	y - r10*x - r11*y - r12*z
r20	r21	r22	z - r20*x - r21*y - r22*z
0	0	0	1

So the rotational components are the same but the rotation moves the position of the centre.

---

Further Reading

You may be interested in other means to represent orientation and rotational quantities such as:

• Axis and Angle
• Quaternions
• Matrices

Or you may be interested in how these quantities are used to simulate physical objects:

• Kinematics

Screw Theory

Matrix vs. Quaternion