On these pages we look at Bivectors and Covectors, concepts which are similar to vectors and related to them. In both cases there is a sort of duality with vector space. These two entities arise out of different concepts and although they are different they may be related.
Bivectors
Goto this page to read about bivectors, this comes from the ideas of Clifford algebras and Geometric Algebra so see these pages for a more in depth look at these concepts.
Covectors
Goto this page to read about covectors, this comes from the ideas of Tensor Algebra so see these pages for a more in depth look at these concepts.
Bivectors and Covectors in 3 Dimensions
in 3 dimensions bivectors and covectors are related and effectively represent the same concept. We can think of the bivector as being made from the reciprocal basis.
So if we have a vector:
v= A1 e1+ A2 e2+ A3 e3
where:
- e1,e2,e3 = basis vectors
Then if we rotate the basis (e1,e2,e3) then we must rotate the components (A1,A2,A3) in the opposite direction to represent the same vector.
If we now take a bivector:
v1× v2= B1 e2 e3 + B2 e3 e1 + B3 e1 e2
Then if we rotate the basis (e1,e2,e3) then how must we rotate the components (B1,B2,B3) to represent the same bivector?
To illustrate this imagine a directed area (bivector) in the e1e2 plane:
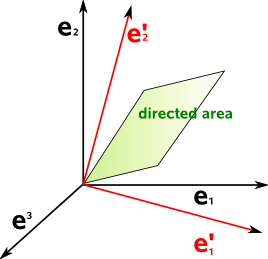
Then imagine that we rotate the basis vectors e1 and e2 around the e3 basis to form e'1 and e'2.
To represent the same parallelogram then the components of the vectors must be rotated in the reverse direction.
However to represent the same directed area then the components of the vectors don't need to be changed, the directed area will change with changes in the normal direction.
So in 3 dimensions there is a duality between vector basis which is contravarient and bivector basis which is covariant.
vector basis contravarient |
bivector basis covariant |
|---|---|
| e1 | e2 e3 |
| e2 | e3 e1 |
| e3 | e1 e2 |
'n' Dimensions
The above only applies in 3 dimensions, in 4 dimensions then bivectors are 6 dimensional so we cant have such a duality, in 4 dimensions there is a duality between vectors and trivectors.
In 'n' dimensions there is a duality between the grades on opposite sides of the binomial triangle. however I have not checked if there is always a parallel contravarient/covariant duality.
Duality

