A Galois Connection is pair of adjoint functors between two categories that arise from partially ordered sets.
let: P = <P, ≤ > Q = <Q, and: f*: P->Q f*: Q->P for all p f*(p) The pair <f*,f*> form a Galois connection between P and Q. |
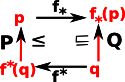 |
Example
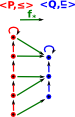 |
Here we look at a perordered set ≤(red) and a mapping to another perordered set (blue). The morphism between them (green) preserves the ordering. That is: if p ≤ p' then f*(p) ≤ f*(p') |
| So is there a mapping (f*) back from Q to P that preserves as much structure as possible in some unique way? | |
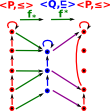 |
Here is a first attempt, as we can see we can compose these morphisms and still preseve the order structure |
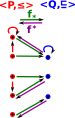 |
So lets add another condition: f*f*(p) ≤ p This condition is not met for our first choice of f* (on the diagram on the left this is interpreted as reversing one of the red arrows). |
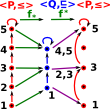 |
However, given the morphism f* then there is a way to choose a way to choose the morphism f* so that the order is preserved relative to the original sequence. For instance, if the number the elements of 'P' with ascending values. We then map these values onto 'Q' using the morphism 'f*'. We can then determine f* by mapping the highest value for each element in 'Q' to the corresponding number in 'P'. f* is then the adjoint of f*. |
