A domain is a particular type if poset.
They come from attempts to give semantics to recursivly defined functions and types.
Example of Application to Computer Languages
| Many computer languages allow us to define functions recursively, for example 'factorial': | factorial(n)
if (n=0) return 1
otherwise return [ n × factorial(n-1) ] |
Types can also be defined recursively like this:
A list could be implemented like this: L(x)=1+x•L(x) = 1+x+x²+x³... see page here |
How can we be sure that these recursive definitions always return a valid result?
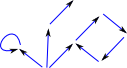
These recursive definitions tend to have a common form:
- A partial function (in above case: 'if n=0, return 1').
- If partial function is undefined then call self.
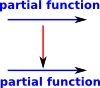 |
In this diagram the blue arrows represent partial functions and the red arrow represents one level of recursion. |
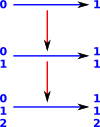 |
So we can see in the factorial example, at each level of recursion the partial function becomes less partial. So these partial functions form a chain: P0 |
Denotional Semantics
We use double square brackets '[[' and ']]' to represent semantic braces. These surround some expression to represent the result of that expression.
As an example imagine that we have a system for calculating the results of a numerical calculation. The syntax is defined inductively as follows:
term ::= number | term + term | term - term | term * term | term / term
where
number ::= 0,1,2,3,4,5,6,7...
We then use the semantic braces to represent the semantics. In this case every term evaluates to a number:
[[term]] = number
The point of denotional semantics is to define how this is done, so we break this down.
For example '3' evaluates to 3:
[[3]] = 3
In fact any number literal evaluates to that number:
[[number]] = number
Here we use 'number' to represent any number, we don't want to do that sort of thing too often or denotional semantics wouldn't add anything at all, here we have to do this otherwise we would have to define every number.
we define the operations like this:
[[a+b]] = [a]+[b]
Unfortunately we have used the '+' symbol for two different things here. On the left it is just a syntactical operation, on the right it is the mathematical operation of add.
This is a very simple example, we now want to go on to show how this can define recursive functions, but first we compare with similar looking approaches.
LogicDenotional semantics seems similar to logic, for instance there are rules like modus ponens: from A and A -> B infer B However not all logic rules lead to a simplification |
Lambda CalculusLambda calculus has variables which we can replace with the actual values during evaluation. |
Partial Functions
When we discussed mappings and functions, on the page here, we will mostly assumed that every element in the domain mapped to an element in the domain, however this is not the case for partial functions.
Examples of partial functions, in the real numbers, are:
- x->1/x (not defined for x=0)
- x->sqrt(x) (not defined for negative numbers)
This is also interesting in computing where a function may represent a computation. Where this computation is very complicated it may not be possible to be sure that every input to the function will produce a valid result.
| On the right is a representation of a partial function as a graph. The function 'f' is defined for inputs 'a' and 'c' but not 'b' and 'd'. |  |
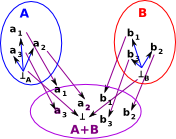
Here is another partial function 'g'. This is related to the function 'f' above because, if defines everything that 'f' defines but it also defines a result for 'b'. This situation where function 'g' is defined as-well-as-or-better than 'f' is represented symbolically as: f |
 |
We can define a whole 'chain' of partial functions. e Below 'f' we have a partial function which specifies an output for a single input, we can build up results upto a compete function. |
 |
At the bottom of this chain we have a partial function which does not map any of its elements. We denote this by the 'bottom' symbol: '
|
 |
A partial function can be made into a total function in various ways:
- We could choose a subset of the domain which is mapped to the codomain
- We could add an element to the codomain to represent 'undefined' then all undefined values can be mapped to this.
The first option may not be possible because we may not know which values have valid results or such a subset may be difficult to define.
Partial Function in Category Theory
A partial function from A to B is defined by the span shown on the left.
Note: an arrow from A to B is not shown since arrows represent total functions. |
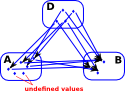 |
Domains
A domain is a poset where:
- Various types of joins exist (a kind of co-completeness property).
- The element
 (bottom element) exists.
(bottom element) exists.
Examples of such domains are ωcpos and dcpos.
Applications
This has been used in defining the semantics of programming languages (denotational semantics). Particularly recursively defined functions.
Recursively Defined Functions
Example Factorial
For example we could define factorial like this:
fact = λ n . if n=0 return 1 else return n*fact(n-1)
The recursion comes because the function is used in its own definition.
| This generates a linear sequence of values where each one depends on the previous one. |  |
| Alternatively we could draw it as a sequence of ordered input-output pairs like this: | 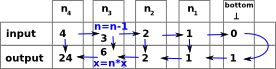 |
| The denotion for a recursive function is a set of ordered pairs, in this case: We could think of this chain as a set of points on a graph. In this case: graph(factorial) |
{[ |
The least upper bound of this chain is the factorial function.
So a recursively defined function can be understood in terms of a family of non-recursive denotions.
Fixed Point Property
Above we defined the factorial like this:
fact = λ n . if n=0 return 1 else return n*fact(n-1)
So 'fact':N->N is the factorial function from N to N, given a number it will return the factorial of it.
But we could treat this like an equation where 'fact' is the unknown.
F = λ fact . λ n . if n=0 return 1 else return n*fact(n-1)
Now we take 'graph' to represent a graph like inputs on one axis and outputs on another and the relationship shown by a subset of the plane. In this case graph is:
{[![]() ] [1 1] [2 2] [3 6] [4 24]...[n !n]}
] [1 1] [2 2] [3 6] [4 24]...[n !n]}
For fixpoint we have:
graph(F(fact)) = graph(fact)
F(fact) = fact
where:
- F: (N+ -> N+) -> (N+ -> N+) is a 'functional' (a function from one function to another).
- fact:N->N is the factorial function from N to N.
- N is natural number
- N+ is extended natural number to include
 .
.
So each level in the recursion only defines part of the function:
- First level: {[
 ] [0 1]} only defines output for input of 0.
] [0 1]} only defines output for input of 0. - Second level: {[
 ] [0 1] [1 1]} only defines output for input of 0 or 1.
] [0 1] [1 1]} only defines output for input of 0 or 1. - Third level: {[
 ] [0 1] [1 1] [2 2]} only defines output for input of 0,1 or 2.
] [0 1] [1 1] [2 2]} only defines output for input of 0,1 or 2. - Forth level: {[
 ] [0 1] [1 1] [2 2] [3 6]} only defines output for input of 0,1,2 or 3.
] [0 1] [1 1] [2 2] [3 6]} only defines output for input of 0,1,2 or 3. - ...
More about fixpoints on the page here.
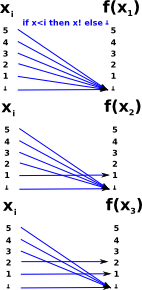
LUB (Least Upper Bound) Lemma
Every chain fi has a least upper bound.
ExampleThis example illustrates a least upper bound although the function is not defined in a recursive way. We define a chain of functions fi: f1,f2,f3... So fi The least upper bound is the factorial function: x->x! |
 |
Functionals
A 'functional' maps a set of functions (with a given signature) back to itself. Possible properties that functionals may have: |
 |
Monotonicityif f for all f,g |
|
Continuityτ[lub{fi}]=lub{τ[fi]} where:
|
Data Types
We can make existing datatypes (initial algebras) into denotions as an extension.
We add bottom (![]() ) to datatypes to represent unknown value. This allows the functions to be partial. So:
) to datatypes to represent unknown value. This allows the functions to be partial. So:
- a->
 means the value is undefined for argument 'a'.
means the value is undefined for argument 'a'.  -> a means we are giving a value to 'a'.
-> a means we are giving a value to 'a'.
Sometimes if we are extending a domain 'D' then we denote the extended domain as 'D+'
For example boolean values: Note: for all these extended domains there is an identity arrow from every element to itself, but I have not shown that on the following diagrams to avoid clutter. |
|
Or Natural Numbers: Here we have two levels of ordering:
|
Example in reals:
inverse = λ x . 1/x
so, for inverse, we have 0->![]()
Combining
| Bottom | Information Ordering | |
|---|---|---|
Product We can take the
|
If:
|
If:
|
Sum |
|
|
| Exponent (function) |
 |
For f,g f 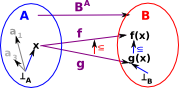 |
On these diagrams the purple arrows represent the underlying relation and the blue arrows represent the 'less or equally defined' relationship.
Types of product for graphs (Cartesian and tensor) are discussed on the page here.
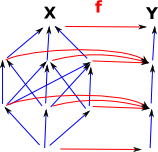
| The product of domains starts to show how we get more complexity and more layers in domains. |  |
Natural ExtensionIf we combine all nodes with at least one A morphism where any nodes with a |
 |
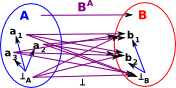
The elements of the exponent BA are all the possible arrows from A to B.
- Those arrows which don't involve
 represent the mappings between A and B.
represent the mappings between A and B. - Those arrows which end at
 B represent undefined mappings so we can represent partial mappings.
B represent undefined mappings so we can represent partial mappings.
Meaning of these Elements in Denotational Semantics
Arrow
If we have an arrow such as A->B the following notation: A![]() B is often used, even when we don't necessarily mean that A is a subset of B. However to make the distinction clearer, here we will use a squared off form of this notation: A
B is often used, even when we don't necessarily mean that A is a subset of B. However to make the distinction clearer, here we will use a squared off form of this notation: A![]() B. This tends to mean that:
B. This tends to mean that:
- A is less defined than B
- or A approximates to B
The relation A![]() B is:
B is:
- reflexive A
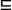 A
A - transitive A
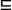 B and B
B and B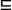 C implies A
C implies A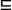 C
C - anti-symmetric A
 B and B
B and B A implies A=B
A implies A=B
Bottom
The denotion '![]() ' often represents a computation that is undefined or fails to terminate.
' often represents a computation that is undefined or fails to terminate.
Extended Domain
So far the extended domain has only 2 levels, that is, there is a direct arrow from![]() to every other element. When we define structures recursively then we get more structure, we get a whole chain where each element is more defined.
to every other element. When we define structures recursively then we get more structure, we get a whole chain where each element is more defined.
Partially Defined Functions
In the S=set {0,1,2} we define a minus '-' function as follows: Since we don't have negative numbers some of the operations will be undefined. |
|
|||||||||||||||||||||||||
| We can make the function fully defined we can extend S to S+, we do this by adding |
|
Domain Theory
 |
As Partially Ordered Set
here we look at a poset represented as a directed graph (like Hasse diagram).
If we have a finite directed graph and we repeatedly follow the arrows then we will eventually get to either:
|
 |
If we have a meet-semilattice then we will always end up eventually at the maximal element. If we have a join-semilattice and we go in the reverse direction to the arrows, then we will always end up eventually at the minimal element. |
 |
| Above diagram redrawn here as a sequence of maps. Each row represents a map D -> D. |  |
Definitions
| Directed Set (or directed preorder) |
set with reflective and transitive binary relation (partially ordered sets need not be directed) |
| dcpos | Directed co-complete partial order. |
| ωcpos | ω-chain co-complete partial order. A poset in which every ω-chain has a supremum |
| chain | For every x,y Sometimes chain is used as another name for 'totally ordered set'. It can also be used for a totally ordered subset of a poset. |
| ω-chain | Its elements can be indexed by the natural numbers. |
| anti-chain | For every x,y |
| complete | existence of meets for subsets |
| co-complete | existence of joins for subsets |
Functions between Preordered Sets
A function between preordered sets preserves structure, in this case the order, this is also known as a monotone function.
A function between preordered sets is:
|
 |
Algebraic Closure System
Algebraic closure systems are systems of subalgebras of finitary algebras (sets with a family of finitary operations).
Given:
- Set 'A'
- Set 'C' of subsets of 'A'
Closed under the intersection of arbitrary subcollections is called a closure system over 'A'.
If 'C' is also closed under the union of subcollections that are upward directed then it is an algebraic closure system.
An algebraic closure system forms an algebraic lattice under the set theoretic inclusion order.