In physics we have equations like T= r × F which apply independently of the position and orientation of the object to which it applies. The equation is also independent of the origin and direction of the coordinate system that we are using.
Ultimately we often need to get results in meaningful coordinates in the physical world although when we are working with physics equations we want our equations to be as general as possible.
We can think of this as different layers and different types of physics give us alternative ways to bridge between those layers:
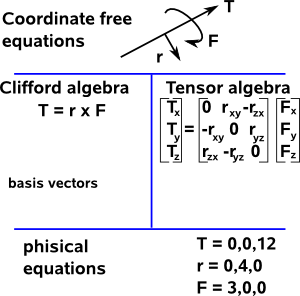
There are many types of algebra that we use in physics but they tend to cluster into two types depending on how they map between coordinate free and physical representations:
In Clifford algebras we tend to express or equations in terms of the basis vectors: e1,e2,e3… and since these basis vectors are part of the equations then we can automatically map back to the physical coordinates.
In tensor algebra we classify the indices as contravariant or covariant and notate them as subscripts or superscripts so that we can keep track of how the physical equations change with different coordinate systems.

