Maths - Limits and Colimits

Limits and Colimits

A limit is a way to take a diagram and encapsulate its properties into one object as simply as possible.

This is a generalisation that includes:

initial/terminal objects
(co)products
(co)equalizers
pullbacks/pushout.

Catagorical Limits

Generalises universal constructions such as:

products
pullbacks
inverse limits

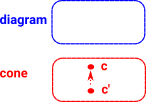
In some category C we have:

A diagram, defined below, for now we can think of as a 'shape' containing objects and morphisms of C.
An object which has morphisms to all the objects in the diagram.

Everything constructed like this is supposed to commute.

This is called a cone.

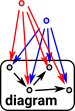There may be other objects that have morphisms to all the objects in the diagram.

The limit chooses the 'best' one.

In this case the 'best' one is the cone which all the others factor through.

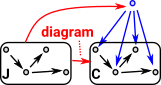To make this more rigorous and categorical we need to define the diagram better.

A diagram of shape J in C is a functor from J to C

More about limits on page here.

Limits

These generate a construction (c) which depends on the diagram such that:

All triangles commute.
Any other object c' can be factored through c without loosing information (there is a unique arrow to make the cones commute).

The first condition makes 'c' general enough to capture the essence of the construction.

The second condition makes sure that it is only just general enough (no junk).

Universal Construction

Universal Cones over Diagram:

terminal

This is a cone over an empty diagram.

Therefore the diagram puts no constraints on c. It is the most general object and so any other object can map to it.

empty diagram

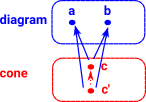
product

objects 'a' and 'b' are independent of each other so c needs to be general enough to contain the information in both.

More about product on this page.

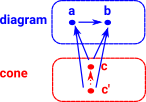
arrow

Not a necessarily universal construction but I've included it here for completeness. Here there is an arrow between 'a' and 'b' so they are no longer independent.

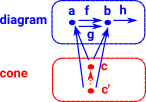
equaliser

'c' is a subobject of 'a' on which 'f' and 'g' agree. Monics are equalisers in set or any topos.

injective function goes from 'c' to potentially larger objects 'a' and 'b'.

In set an injective function defines a subset relationship. In category theory this can be generalised to a monomorphism (monic).

if h•f=h•g then f=g

(h on left cancels out if monic)

More about equalisers on this page.

pullback

More about pullback on this page.

Colimits

universal cone over diagram:

Initial

empty diagram

Sum

More about sum on this page.

pushout

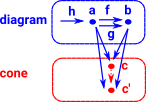
coequaliser

In set an surjective function defines an equivalence relationship. In category theory this can be generalised to a epimorphism (epi).

if f•h=g•h then f=g

(h on right cancels out if epi)

Shows which elements of 'a' are equal to other elements of 'a'. (Can be represented by some subset of a×a).

More about co-equalisers on this page.

Limits and CoLimits in Set

Just to give some intuition here are some diagrams showing the internal set structure.

	universal cones over diagram:
terminal not sure how to show this
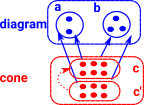
product objects 'a' and 'b' are independent of each other so c needs to be general enough to contain the information in both.
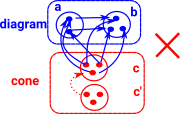
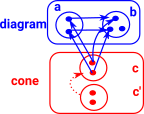
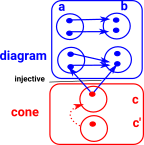
arrow injective In this example we cant make the triangle commute with a 3 element set in cone.

arrow surjective
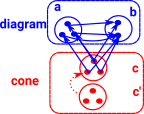equaliser 'c' is the subset of 'a' on which 'f' and 'g' agree.
co-equaliser Surjective function merges back those elements that don't commute.
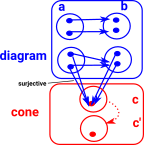pullback