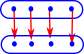
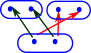
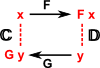Maths - Category Theory - Comparing

Maths - Category Theory - Comparing Objects

When comparing objects it is often more interesting when two sets are not identical but preserve some form of structure when mapping between them.

relative strength

type and category notation

description

tightest

Equality

C and D are the same in these terms

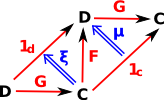
Isomorphism
1_d = GF
FG = 1_c

There must be an arrow and inverse between the objects and when composed these give the identity map for every element.

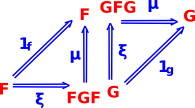
Equivalence
1_d

GF
FG

1_c

equivalence triangle

For equivalence there is a arrow in both directions between the two objects. It is not necessary that GF and FG are the identity elements but they must be isomorphic to the identity elements.

loosest

Adjunctions

adjunctions
unit:
μ : 1_c =>GF
co-unit:
ξ : FG => 1_d

triangle identities:	as 2-cells:

For adjunctions there is a arrow in both directions between the two objects. It is not necessary that GF and FG are the identity elements but only that they have natural transformations to the identity elements.

FG is unit (does not change object - injective followed by surjective) but GF does change object (surjective followed by injective). Like equivalence but in one direction.

Alternative definition: there is an isomorphism:
φ: D(FA , X) -> C(A, GX)
for every AC and XD

Equivalence Relations

In a less category specific approach to binary relations they may, or may not, have the following properties:

Equivalence Relation

Group

transitive

reflexive

symmetric

Comparison of Sets

Here we investigate this comparisons with the simplest concrete categories - sets.

type of comparison	Sets	GF
Equality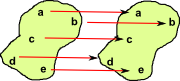
Isomorphism 1_d = GF FG = 1_c
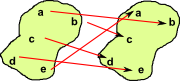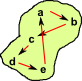Equivalence 1_dGF FG1_c
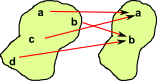Adjunction

More Detail

EuclideanSpace

home

About This Page

This is one of a series of pages about category theory.

This section is about types of equality-like relationships in category theory.

See this page about 'equality' between 'elements.

These pages discuss various types of 'equality' between categories:

Equality

In Set Theory More on page here.		Two sets are equal if they contain the same elements (Principle of Extensionality). If the set has structure then that would also have to be equal in some way.
In Category Theory More on page here.		Often when comparing types we need some loser way of considering that two types are essentially the same. Isomorphism is frequently the most appropriate type of equality. This is defined using a category theory way, that is, by external morphisms.
In Type Theory More on page here.	vec(x)=vec(x+0)	In M-L type theory the Identity type is often used. If things are equal in this way they can be interchanged when used in computer programs.
In Type Theory More on page here.		In Homotopy Type Theory (HoTT) there is a different way to get isomorphism from equality. That is to allow types to be equal in many ways.

metadata block

see also:

catsters youtube video - Adjunctions 1 - The notion of an adjunction. Definition via unit and counit natural transformations and the triangle identities.
catsters youtube video - Adjunctions 2 - Definition of adjunction via natural isomorphism between hom-sets. Getting the unit and counit from this.
catsters youtube video - Adjunctions 3 - Adjunctions give rise to monads.
catsters youtube video - Adjunctions 4 - The two notions of adjunction coincide.
catsters youtube video - Adjunctions 5 - Every monad comes from an adjunction via its category of algebras.
catsters youtube video - Adjunctions 6 - Definition of the Kleisli category.
catsters youtube video - Adjunctions 7 - The adjunction coming from the Kleisli category. The category of adjunctions for a monad: the Eilenberg-Moore and Kleisli categories as terminal and initial objects.

Adjunctions from Morphisms

catsters youtube video - Adjunctions from Morphisms 1 - Motivation for the construction of adjoint functors for bundles over sets
catsters youtube video - Adjunctions from Morphisms 2 - The category of bundles on a set as a slice category and as a functor category into sets.
catsters youtube video - Adjunctions from Morphisms 3 - The definition of the pull-back and its right adjoint for bundles over sets.
catsters youtube video - Adjunctions from Morphisms 4 - A proof that the push-forward is right adjont to pull-back.
catsters youtube video - Adjunctions from Morphisms 5 - Description of the left adjoint to the pull-back

Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

The Princeton Companion to Mathematics - This is a big book that attempts to give a wide overview of the whole of mathematics, inevitably there are many things missing, but it gives a good insight into the history, concepts, branches, theorems and wider perspective of mathematics. It is well written and, if you are interested in maths, this is the type of book where you can open a page at random and find something interesting to read. To some extent it can be used as a reference book, although it doesn't have tables of formula for trig functions and so on, but where it is most useful is when you want to read about various topics to find out which topics are interesting and relevant to you.

Terminology and Notation

Specific to this page here:

This site may have errors. Don't use for critical systems.