Maths - Concrete Categories

On these pages we look at concrete categories. Concrete categories are a set together with some form of 'structure' such as functions and operations within the category. (ref nLab).

Although category theory does not look inside objects I want to be able to translate between category and (for example) set theory. It seems to me that, to really understand a mathematical topic, it helps to be able to approach it from many directions.

So, although we don't look inside objects and arrows, to get some intuition it helps to take a peek.

Also its not practical to do everything in category theory so we still need to translate between different approaces. After all, if an engineer is calculating the loading of a bridge, they probably don't want to calculate it 'up to isomorphism'.

Examples

Category	Internal Category		Notes
Category	Objects	Arrows	Notes
Set See page here for more.	1,2 ... n elements A container with no internal structure.	functions (possibly injective/surjective)	All structure comes from the arrows.
Group	One set and (possibly) multiple endofunctions. These must be permutations.
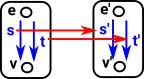
Directed Graph See page here for more.	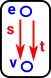Two functions, source and target) from the set of edges to the set of verticies.	Two functions, between the source and target arrows, which respect the graph structure.	An example of a functor category.
Natural Numbers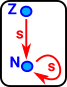

Categories and Types

So lets look at how objects and arrows in category theory may, or may not, relate to types and terms in type theory.

In type theory we have types and terms (and perhaps a higher level type constructor) so a sort of three layer hierarchy. In category theory:

The type constructor might correspond to the category (FinSet category)
A type might correspond to an object in category theory.
A term (element of the set) is not explicitly referenced in category theory (we only look at the external properties, not what's inside it).

Consider finite sets:

FinSet

In a finite set category objects are:

The empty set.
A one element set
A two element set
A three element set
...

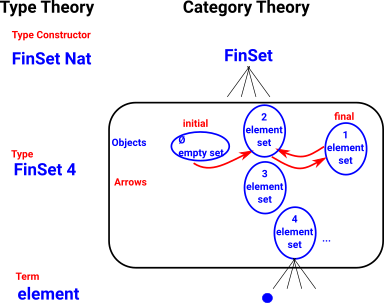The arrows are the mappings between these objects.

Of course category theory does not look inside objects or arrows to see the elements but, to try to give better intuition, lets make an exception in this diagram:.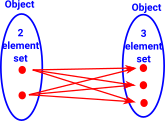

For further discussion of the properties of sets in category theory see this page.

Natural Numbers

Not all catergories relate to type theory in the same way as FinSet.

In the case of natural numbers:

Types map to objects.
Terms map to arrows.

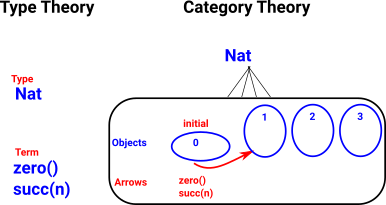Monoid

In set there were few restrictions on arrows (apart from no arrows to empty set).

However when we add extra structure to the set this puts constraints on what arrows we can have.

We can think of a monoid as a set with some extra structure . So we can start with an underlying set then represent the monoid operation by arrows which constrain what is allowed to comply with the axioms.

However the monoid category is more usually modeled as a single object with multiple arrows from and back to itself (endo-functors).

Other Concrete Categorories

Graph

Finite Categories

Name	Diagram	Description
0		No objects No arrows
1		One object The only arrow is the arrow back to itself (identity arrow). For instance: if the object is 'set' then the whole thing is a monoid.
2		Two objects here are some examples:
		1+1 that is the disjoint union of two single objects
		This could be an index category
		This could be a graph
3		Three objects. The arrow from first to last is implies by the composition law.

Here we avoid loops (exept identity) which would mean that something else is going on (such as isomorphism or adjunctions).

Preorder

In set theory (see page here) a preorder is a set equiped with a binary relation '<=' which is

reflexive: a<=a
transitive: if a<=b and b<=c then a<=c

In category theory a preorder only has, at most, one arrow between any two objects.

So, if an arrow exists it is uniquely determined.

Categories with binary operation and identity element

	single objects	multiple objects ->
		composition law	no composition law
invertible	Groups	Groupoids all morphisms are isomorphisms	Graph
non-invertible	Monoids	Categories	Directed Graph

Illustrating Category Constructions

In order to get an intuitive understanding of category theoretic constructions I find it helps to use examples from the simplest concrete categories to show what is going on internally, especially if it can be illustrated graphically. Of course, we are not really supposed to look inside categories, but I think its necessary to get an intuitive understanding.

Often sets are the simplest category to show whats going on.

If sets don't have enough structure the a pre-order (see this page) is often a good example to use (on this page I have tried to use preorders to show the idea of adjunctions). pre-orders are good because of the graphical nature of Hasse diagrams.

Pre-orders are also good because they are a specific (less general) case of categories in that, like categories, they are reflexive and transitive:

reflexive

a≤a

If a relationship is reflexive then there is always an arrow from an element of a set to itself. Although when drawing the Hasse diagram we may not draw it to avoid clutter.

transitive

if a≤b and b≤c then a≤c

This is like composing functions. That is: if the is an arrow from 'a' to 'b' and an arrow from 'b' to 'c', then we can attach the tip of the first arrow to the second arrow to get an arrow from 'a' to 'c'.

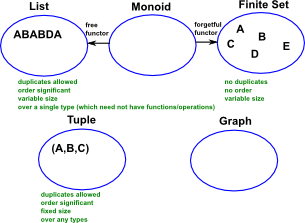On these pages we look at concrete categorories. A definition of concrete categorories is a set together with some form of 'structure' such as functions and operations within the category. (ref nLab)