Maths - Category Theory - Arrow

Arrows

In category theory diagrams arrows represent structure preserving maps (morphisms) between objects. The direction of the arrow is significant and there is no assumption of an inverse.

There may be multiple arrows between any two elements ()

In general, an arrow might represent many possible morphisms (see homset) although we may require that certain arrows be unique (see universal properties) given the other arrows, these are sometimes shown as dotted arrows.

In this diagram: the arrow A->B and the arrow B->C implies the arrow A->C so it does not need to be explicitly shown unless there is a requirement for the triangle to commute.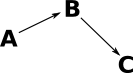

Therefore it is not usually necessary to show two arrows in parallel unless we are defining higher order properties (natural transformation in a 2-cell).

Unless otherwise stated: objects in a diagram are usually defined 'upto isomorphism' so arrows don't have to be defined beyond that, however some things are defined 'upto equality':

The Id arrow from an object to itself, this does not change the object (its not a permutation).
When there is a requirement for a diagram to commute, then this means that both paths produce exactly the same result (although the objects themselves are not defined beyond isomorphism).
If the arrows form a loop (in the direction of the arrows) then there are usually additional conditions.

Types of Arrow

Sometimes we have specific notations for types of arrows:

Morpism	AB	A structure preserving map between two objects
Injective	AB	Sometimes we want to denote that a morphism is injective, so we add a hook.
Unique	AB
Element	a b	Its not really in the spirit of category theory to define arrows in terms of elements. However it can still be useful to explain the diagram.
Hom Set	AB	There isn't really a recognised symbol for multiple arrows, often homset type arrows are drawn as a single arrow. However I find it useful to draw multiple arrows, specially in a representable type of situation. See page here for more about hom sets.
Natural Transform	AB	A natural transformation is drawn as a double line between two morphisms. See page here for more about natural transformations.
Functor		Usually a functor is drawn as a single arrow, like a morphism just between categories, here I have drawn it like this to stress how it preserves structure. See page here for more about functors.
Representable Covarient		Not perhaps usual notation but its useful to show how an element of X can pick out an individual morphism in the hom-set. See page here for more about representables.
Representable Contravarient		Same as above.

Inside Arrows

The following are not the 'arrow diagrams' that we usually work with in category but an attempt to show the type of internal structures that the arrows could represent, this type of detail is abstracted away by category theory to look at a higher level structure:

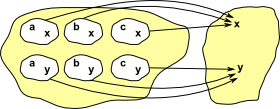	Here I have showed individual arrows going from each element of the two objects rather than the more usual single arrow between the two objects.
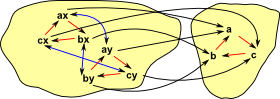	In the case of groups we may be able to give an indication of how the group operation is changed by the arrow.

We will call the object at the start of the arrow the 'domain' and the object at the end of the arrow the 'codomain'

Homsets

The above diagrams show a single morphism 'inside' the arrow, however a more general case is that there could be a whole set of morphisms represented by the arrow, this is known as a homset.

If we need to show how objects of category get mapped, then we can use a notation like:

hom(a,b)
where:

a is an object in the domain A
b is an object in the domain B

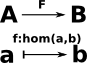Alternative notations are:

hom_C(a,b)
C(a,b)
(a,b)
(a,b)_C

where:

a is an object in the domain A
b is an object in the domain B
C is the category.

Homsets compose, corresponding to the arrows they relate to:

hom(b,c)hom(a,b) -> hom(a,c)

The '' symbol is not usually used but it reminds us that homset composition is bilinear and so is a tensor product.

more here

Exponentials

So an arrow potentially represents multiple morphisms, how many?

given f: A -> B

and no other information, then there are B^A. That is,

fB^A

Types of Arrow Related to Set Category

Although the ethos of category theory is to define things externally to objects, when we are trying to get an intuitive understanding of the subject it helps to look at concrete categories and compare internal (arrows between elements) and external (arrows between objects). So here we look at various types of arrow in finite set category. There os more information about finite set category on this page including a discussion of reverse of the arrows.

Arrows Between Finite Sets

Arrows Between Categories (structured)

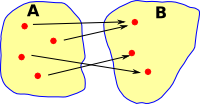
injective

Every element in the domain is the start of an arrow which goes to a unique element in the codomain

This function is reversible but if we apply the reverse function first and then this function we don't necessarily get back to where we started.
f ^-1 f =1

monic (monomorphism)

fg = fh implies g = h

examples in concrete categories:

category	meaning
set	subset
group	subgroup
vector space	subspace

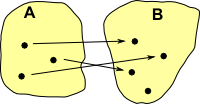
surjective

Every element in the codomain has at least one arrow leading to it and possibly more than one.

This function is not necessarily reversible, however if we apply the reverse function first and then this function we get back to where we started.
f f^-1 =1

epi (epimorphism)

if = jf implies i = j

examples in concrete categories:

category	meaning
set	equivalence classes
group	quotient group
vector space	quotient space

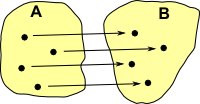
bijective

Each element in the domain maps to a single element in the codomain. This creates a 1:1 correspondence between elements in the domain and codomain.

This function is reversible:
f f^-1 = f^-1 f =1

isomorphism

both fg = fh implies g = h
and if = jf implies i = j

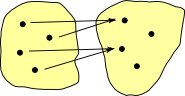
non-injective and non-surjective

some elements in the codomain don't have arrows leading to them and others have multiple arrows.

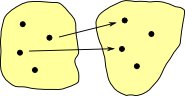
partial

This is not really a valid function as the above examples are because some elements in the domain don't have arrows. However this can be modeled as a function by using the 'maybe' monad as discussed on page here. Partial functions can be represented by arrows in category theory.

Definitions:

If f: A -> B then:

a retraction for f is a map r: B -> A for which r o f = 1_A
a section for f is a map s: B -> A for which f o s = 1_B
an endomap e is called idempotent if e o e = e
an automorhism is both an endomap and an isomorphism.

We can lift the concept of an arrow up to the next level by constructing an arrow category as discussed on this page.