 |
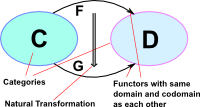
A natural transformation is a mapping between two functors. The functors must have the same domain and codomain as each other. There is also the natuality square condition that must apply for this to be a natural transformation as we shall see below. |
Components
For components we will be working in terms of internal objects:
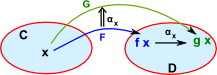 |
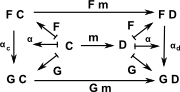
ComponentsFirst we take an object 'x' in 'C' and we see that this maps to a morphism in 'D'. For every object 'x' in C there is a morphism in D (f x -> g x) known as the components of α at x written αx. |
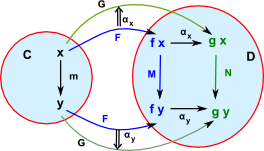 |
Natuality SquareSo now we know what happens to on object in 'C', we now want to know what happens to structure in 'C', for this we see what happens to a morphism in 'C'. A morphism in C would map to two component morphisms in D. This diagram must commute for every morphism in C. So αx is the component of the natural transform at x and αy is the component of the natural transform at y. For naturality we require that the square in D commutes, that is, αy• M = N • αx where: M = F m so: αy• F m = G m • αx |
Here is a more schematic view of the For a natural transformation α: F -> G |
|
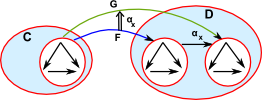 |
2-CategoriesWe could generalise this to any structure in C which would have two components in D. Usually we define categories from the outside using arrows, in this case we look 1 level inside the category, two layers of category are known as a 2-category. |
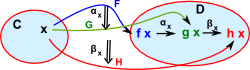 |
Composition VerticalWe can apply α to F to get G and then β to get H. |
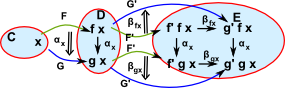 |
Composition Horizontal
|
Horizontal and Vertical Composition
So a natural transformation adds another layer on top of functors. When we looked at functors we saw that we can see them at two levels, we can see them in terms of internal objects, or we can 'lift' the view to be in terms of structure.
So how can functors of functors occur? That is functors that map one functor to another, there are at least two ways which I will show here as horizontal or vertical:
| Horizontal | 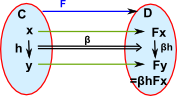 |
The first way that we can get functors of functors is not new, it arises from morphisms. A function of components (x and y) gives rise to a function of the function 'h'. |
| Vertical | 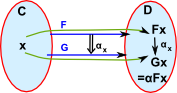 |
The natural transform is shown here as a vertical double arrow. We can 'lift' the view, so that the natural transformation relates the functors F & G in a way that is independent of the underlying categories C & D. So we have a morphism of functors, that is we can regard the functors as objects and α as a functor. |
| Square (combination of horizontal and vertical) | 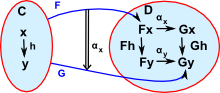 |
The natuality square requirement combines these vertical and horizontal functors into to a square which must commute for naturality. αy º F(h) = G(h) º αx |
or if we notate: βF = F(h) and βG= G(h):
αy º βF = βG º αx
So now we have 3 levels at which we can view natural transformations:
- 0 - Lowest level - In terms of internal objects
- 1 - Mid level - In terms of structure of original categories
- 2 - Highest level - Treating functors as 'objects' and natural transformations as functors.
When working at level 1 and 2 we must remember that the natuality square (see below) applies but when we include the lowest level natuality comes out of the diagram automatically, so we will start by working in terms of the internal objects, until the natuality square becomes intuitive.
Examples
Example - Computer Language Types - Lists
On the functor page we saw how an example of lists (as used in computer languages) could be seen as instances of functors, here we extend that example to natural transformations.
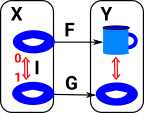
We start with a 'List' functor. This takes any category 'C' and maps it to a category 'List C'. |
|
| For example it maps 'int' to 'List int' and so on, because 'List' is a functor it maps the internal functions of the category. For example 'int' can have a 'negate' function, and we can define 'negate' for 'List int' as negate each element separately. Other categories such as 'string' will have their own functions which will be respected by the list functor. | 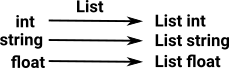 |
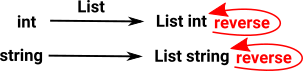 |
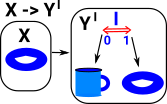
We now want to add a reverse operation to the list which reverses the order of the elements. We could define this for each type of list. |
| But the reverse operation is independent of the type of C so we can just show it like this: | |
 |
However, its important to make it clear that the reverse operation is independent of the internal operations of the categories, therefore we draw it 'orthogonal' to the functor, like this. |
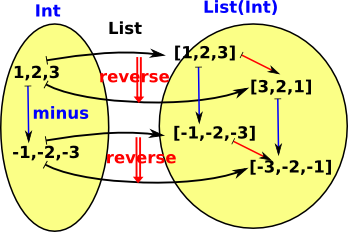 |
Natuality square for List(Int) |
In the case of containers like this:
- Functor (map) does not change container structure but needs to be able to operate on elements.
- Natural transformations change the container structure but do not require a knowledge of the internal structure of elements.
A list may also be thought of as a cartesian product.
Take example 'C' is a set containing elements such as x and y. 'D' contains lists written as [x] for a list with a single element x.
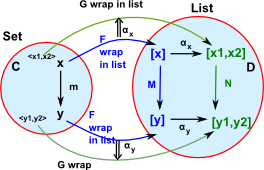
The cartesian product of x1 and x2 in set is mapped to a list containing x1 and x2.
Example 2 - Permutation Groups
As our category with the object being a set and the morhisms being the permutations of the set elements. We can think of composition of these permutations as being a natural transformation. See Yonada lemma. |
 |
Proof
On site here are definitions in Isabella.