There is an alternative to the usual category theoretical diagrams which are 'string diagrams'. We can think of string diagrams as being the Poincaré dual of the usual category theoretic diagrams.
| Category Diagram | String Diagram | |
|---|---|---|
| Objects | point | area |
| Morphism/Functor | line (between objects) | line (separates objects) |
| Natural Transform | double line (between functors) | point (expanded to circle) |
Each type of diagram has pros and cons and the choice of best diagram type probably depends on what we are using it for.
Probably the best way to understand these is to look at some examples below:
The first two examples could have been represented as a one-dimensional string diagram (lines for objects and dots for functors) but I have expanded them into two dimensions to be the same as the other diagrams. there is not much advantage in a one dimensional string diagram. There is no arrow on the string diagram but here the direction is assumed to be from left to right (the convention varies, the Catsters video uses the opposite convention).
| Category Diagram | String Diagram | |
|---|---|---|
| A simple functor |  |
 |
| Functor composition |  |
 |
Natural transformations are shown as dots on a line which are expanded to circles:
| Category Diagram | String Diagram | |
|---|---|---|
| A natural transformation |  |
 |
| Horizontal composition of natural transformations |  |
 |
| Vertical composition of natural transformations |  |
 |
| Horizontal and vertical composition of natural transformations. Implies interchange law: we don't have to define whether horizontal or vertical composition is done first. |  |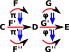
 |
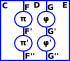More complicated diagrams:
| Category Diagram | String Diagram | |
|---|---|---|
| A loop can be shown by having the same category on the left and the right. The identity map is shown here as a dotted line but it is usually omitted completely. |  |
 |
| Whiskering: G could have natural transform to itself but we don't need to show it. |  |
 |
Adjunctions (more about adjunctions on this page):
| Category Diagram | String Diagram | |
|---|---|---|
| We start with a diagram like this (F is left adjoint to G) and add 2 natural transformations below (η and ξ) with the following axioms. |  |
|
We take this diagram:  between functors and put it in a diagram with the objects. The string diagram has the identity functor omitted as explained above. Also, for simplicity, ξ is not shown in a circle. |
 |
 |
 And again for η. |
 |
 |
 Now for the triangle equalities. In the string diagram it just looks like we can pull the line straight. |
 |
 |
 The other triangle equality |
 |
 |
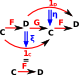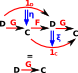Monads (more about monads on this page):
Because there is only one object, it is not shown on the string diagram. So, in this case, crossing over the line means going once round the endofunctor 'T'.
| Category Diagram | String Diagram | |
|---|---|---|
| A monoid is an endofunctor with two natural transformations and axioms shown below. |  |
|
| The first natural transformation μ |  |
 |
| The other natural transformation η |  |
 |
| The left unit triangle |  |
 |
| The right unit triangle |  |
 |
| The associatively square. |  |
 |