Equaliser
In set an injective function defines a subset relationship. In category theory this can be generalised to a monomorphism (monic).
if h•f=h•g then f=g (h on left cancels out if it is monic) |
Coequaliser
In set an surjective function defines an equivalence relationship. In category theory this can be generalised to a epimorphism (epi).
if f•h=g•h then f=g (h on right cancels out if it is epi) |
Injective and Surjective Functions in Set Theory
We are not really supposed to look inside sets in category theory but I find it helps me to get some intuition.
Injective FunctionsIn set an injective function defines a subset relationship. In category theory this can be generalised to a monomorphism (monic). If the injective function is after the pair then: h•f=h•g does imply that f=g. |
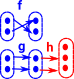 |
EqualiserIf the injective function is before the pair then: f•h=g•h does not necessarily imply that f=g. However an injective function before the pair can form an equaliser, this selects the elements where 'f' and 'g' agree. |
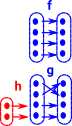 |
Surjective FunctionsIn set an surjective function defines an equivalence relationship. In category theory this can be generalised to a epimorphism (epi). If the surjective function is before the pair then: f•h=g•h does imply that f=g. |
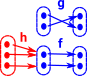 |
Co-equaliserIf the surjective function is after the pair then: h•f=h•g does not necessarily imply that f=g. However an surjective function after the pair can form a co-equaliser, merges the elements where 'f' and 'g' do not agree and so the end-to-end function commutes. |
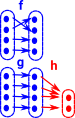 |
Next
This page describes how equalisers can be generalised to limits and coequalisers can be generalised to colimits.