A functor is a mapping between categories which preserves some aspect of the category structure.
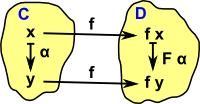 |
In terms of objects of the categoryIf the category is based on an underlying set then we can define the functor in terms of arbitrary elements of the set. As an example take a unary function α: x -> y . If we apply a function (or mapping) from each element of C to a corresponding element of D then this will induce a corresponding function The function 'f' maps an element 'x' in the domain to 'f x' in the codomain, indicated by the black f, in this respect it is just like a function, it also maps 'x' in the domain to 'f y' in the codomain. However the functor also maps 'structure' for instance, it maps the arrow: x -> y in the domain to the arrow: F x-> f y in the codomain, indicated by F. We can just abstract this to F which maps the whole category. In the case of 'f' being 1:1, that is C and D being isomorphic, this gives a square which must commute for a valid functor, that is a functor which preserves structure, which gives: (F α) • f = f •α where • represents function composition. Notes:
|
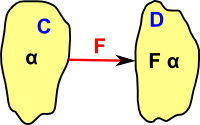 |
In terms of the structure of the categoryThe spirit of category theory is to define things in terms of their external interactions rather than their internal structure. We can 'lift' the above derivation to be purely on terms of structure rather than arbitrary internal objects. A functor is a function from one function to another function, that is, it is a second order function (which conserves structure). At this higher level of abstraction these categories (which are themselves objects and arrows) are compared by means of an arrow called a functor. |
Axioms of a Functor
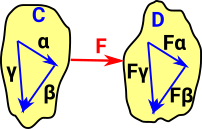
A functor preserves composition and identity. That is:
if γ = α •β then F γ = F α • F β |
 |
| F idα= idFα | 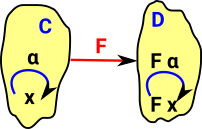 |
Inside Functors
Page about functors here. A functor maps both elements and functions in some category.
In category theory we don't tend to look inside categories (such as the category of set). However I find it helps my intuition to attempt to derive properties of some categories (such as arrow category) from internal properties.
 |
The mapping of functions must play well with the mapping of the elements. g•F= F•f or since g = F f : (F f) • F= F•fwhere • represents function composition. |
 |
Or we could have a contravarient functor: (Ff)-1 • F = F •f |
An alternative approach could be, rather than looking at an individual functor, we could try to look at all possible functions in terms of homsets:
 |
|---|
This can lead to structure in:
- Comma and arrow categories.
- Pre-sheaf, sheaf and Yoneda lemma.
- Fibrations and Grothendiek construction.
Example 1 - Modulo Addition
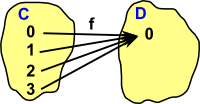
| Here is a functor which is epi (epimorphism). The category C contains the numbers 0 to 3 and the category D contains the numbers 0 to 1. The functor sends the odd numbers to 0 and the even numbers to 1. As it stands this is a pure set category but we can add some structure: | 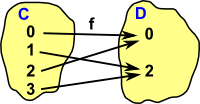 |
| For example the functor F will take modulo 4 addition in C and map to modulo 2 addition in D. | 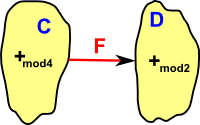 |
See this page for introduction to monic (monomorphism) and epi (epimorphism) functors
Endofunctor
A functor from a category to itself is called an endofunctor.
This is often defined recursively, for example, we can define a functor from List to List which allows one list inside another list. This will produce an infinite sequence of objects:
- List x
- List List x
- List List List x
- ...
Endofunction
An endofunction is a function whose codomain is a subset of its domain.
Finite endofuctions are equivalent to monogeneous directed graph
Example 2 - Lists
| We can think of a list as a free monoid. In computing we tend to think of a list as a functor. | 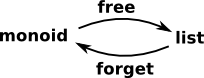 |
Or should the diagram be this? For instance if set is {a,b,c} then list gives us every possible sequence of a,b and c. |
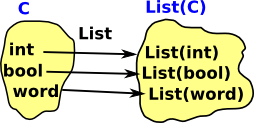 |
List can be considered a functor in that it takes a type such as integer: int and creates a type: List(int). To be a functor it must do more than this, it must obey the axioms of a functor. A functor must also map functions, for instance: List(minus(x)) -> minus(List(x)) |
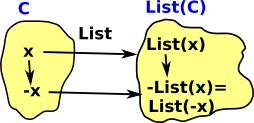 |
So, in the case of a list of integers, we can take a function which returns a negative value. the concept of List is defined in computer languages. Most languages would not have the concept of a minus List but languages that have higher order functions would have a map function which can apply a function like minus to all its values. |
As an example the language Haskell has the following 'map' function for lists:
map :: (a -> b) -> [a] -> [b]
This is specific to lists but in Haskell this can be generalised to any functor 'f':
fmap :: Functor f => (a -> b) -> f a -> f b
More about representing functors in computer languages on page here.
We can extend this example to represent natural transformations as shown on page here. (non category theory discussion of lists here).
Special Cases
Functor to Terminal (or Final) CategoryHere is a more extreme example of the epimorphism example above, virtually all the structure is lost, but it still can be a valid functor. If C and D are groups, for example, then 0d must be the identity and D is the trivial group. If C and D are sets then D can contain no elements (Ø) so that would be the terminal category and there would be no arrows for the elements but if we lift this to the top level we can still have a functor 'F' from C to D.. For more about terminal categories see this page. |
 |
Covarient and Contravarient Functors
 |
Covarient FunctorThis maps objects to objects and arrows to arrows. |
 |
Contravarient FunctorThis maps objects to objects and arrows to arrows in the opposite direction. |
For an example of a contravarient functor set the page about the concrete category 'set'.
Question
I'm not sure about this but I wonder if its possible to have something similar to a functor but which maps objects to arrows and arrows to objects?
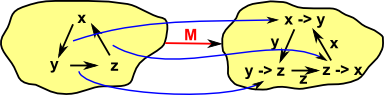 |
Is this possible? |
Functors in Programming
In terms of programming how do we think about functors? If we have a functor from object A to object B should we:
- Think think of the objects as being fixed and then add in the functor to be compatible with the objects?
- Think of the functor generating object B from object A?
In the list endofunctor example above it feels like the endofunctor is generating an infinite series of objects. However if we step up to functors and natural transformations then the functors seem to represent the fixed structure (compile time) and the natural transformations seem to represent the dynamic structure (run time).
Functors in Haskell / Idris
When the word 'functor' is used by programmers I am not sure that it is always used to mean that (and not just an 'arrow - a mapping that preserves some structure although not necessarily between different categories). So, when it maps elements then it preserves functions between those elements, this is usually represented by a 'map' or 'fmap' function. So, is 'List' a functor? It maps between say 'int' and 'List int', are these different categories?
So, in haskell, functor has a type signature like:
(a -> b) -> (F a -> F b)
or since the last bracket is unnecessary: (a -> b) -> F a -> F b
Which represents the functor in terms of the types of the internal objects of the category. So this implements two layers, as discussed already the spirit of category theory is not to work in terms of the internal elements so we want to 'lift' the representation outside the category but it seems difficult to do this programmatically.
The functor needs to map all types of structure, the above signature only appears to map unary functions: a -> b but since Haskell currys the parameters we could make a = c -> d so, due to the currying we would get:
(c -> d -> b) -> (F c -> F d -> F b)
so we can represent all structure, however it would be difficult to do this in most other languages.
More about Haskell on this page.
Proof
On site here are definitions in Isabella.
Further Topics
We go on to look at natural transformations on this page, this adds another layer.