We can think of quaternions as an element consisting of a scalar number together with a 3 dimensional vector. In other words we have combined the 3 imaginary values into a vector.
We could denote it like this: (s,v)
where:
- s = scalar
- v = 3D vector
So the quaternion still has 4 degrees of freedom, its just that we group the 4 scalars as 1+3 scalars, the quaternion is still an element but the vector is a sub-element within it (if that's not a contradiction in terms).
One advantage of sub-grouping the quaternion in this way is that it simplifies the relationship between quaternions and axis-angle representation of 3D rotations.
As discussed here, a quaternion can be represented in terms of axis-angle, in the usual notation this is:
q = cos(a/2) + i ( x * sin(a/2)) + j (y * sin(a/2)) + k ( z * sin(a/2))
where:
- a = angle that we are rotating through
- x,y,z = unit vector representing axis
Converting this to scalar & vector form simplifies this as follows,
q = (s*cos(a/2), v *sin(a/2))
If this represents a pure rotation
q = (cos(a/2), axis*sin(a/2))
where:
- a = angle that we are rotating through
- axis = unit length axis vector
An advantage in using a vector to build a quaternion is that we can use vector algebra on it. Imagine a point P1 which is a unit distance from the origin, we will be rotating it through an angle (a) to P3 through midpoint P2.
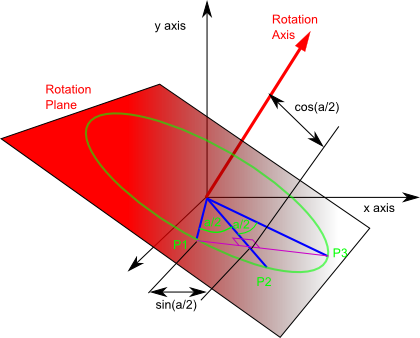
This diagram is explained here.
If we take the cross product of P1 and P2 we get a vector along the rotation axis, because it is mutually perpendicular to both, and since P1 and P2 are on the unit length circle the cross product will be unit length so:
P1 × P2 = axis
where:
- P1 = initial position of a point being rotated
- P2 = position of point after being rotated half way (through a/2)
- P3 = position of point after being rotated through angle a
- × = cross multiplication operator
- axis = unit length axis vector
Similarly cross multiplying P2 and P3 will give exactly the same vector:
P1 × P2 = P2 × P3 = axis
We can now try the dot product, as explained here, if A and B make angle theta :
A•B = |A| |B| cos(theta)
Since P1 and P2 are unit length:
P1•P2 = cos(a/2)
Similarly with P2 and P3:
P1•P2 = P2•P3 = cos(a/2)
Therefore:
q = (P1•P2, P1 x P2)
Note: P2 is the mid point of the rotation, if we want this in terms of the endpoint vectors we could substitute:
P2 = (P1+P3)/ |P1+P3|
So this gives the quaternion representing the rotation in terms vectors representing a point being rotated. However, we frequently want to do the reverse of this, often we already know the quaternion representing the rotation and we want to know how this will transform a given point.
To do this we will create quaternions representing the the vectors by setting the scalar part to zero, so we let,
- q1 = (P1,0)
- q2 = (P2,0)
- q3 = (P3,0)
From this page we know:
q*q1 = q2
and
q' = q2*q3'
multiplying these together gives:
q*q1*q' = q2*q2*q3'
q*q1*q' = -q3'
q*q1*q' = q3
Arithmatic Using Scalar and Vector Notation
On this page we defined quaternion arithmetic in terms of qw, qx, qy and qz but we can also define the arithetic operations in terms of scalar and vector notation:
(sa,va) + (sb,vb) = (sa+sb,va+vb)
(sa,va) - (sb,vb) = (sa-sb,va-vb)
(sa,va) * (sb,vb) = (sa*sb-va•vb,va × vb + sa*vb + sb*va)
(sa,va) / (sb,vb) = (sa*sb+va•vb,-va × vb - sa*vb + sb*va)
where:
- (sa,va) = quaternion a
- (sb,vb) = quaternion b
- • = vector dot product
- × = vector cross product