Introduction
The multiplication rules for complex numbers make them suitable for representing rotational quantities in two dimensions. Of course we can represent a 2D rotation as a single number representing the angle of rotation in degrees or radians, combining subsequent rotations can be done by adding the corresponding angles.
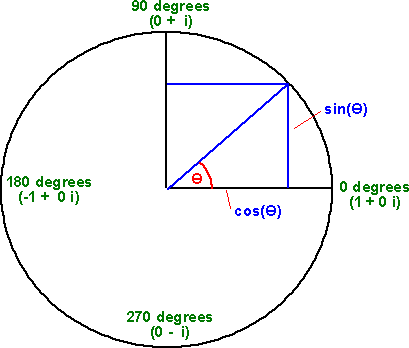
However we often need to work with the two dimensional components of the rotating quantity. It would be a big overhead to convert back and forth between the angle and components, especially as these involve trig functions as follows:
Angle to complex:
real = cos(angle)
imaginary = sin(angle)
Complex to angle:
angle = atan2(real,imaginary)
Complex numbers can often remove the need to work in terms of angle and allow us to work purely in complex numbers. For example if we have an orientation, represented by a complex number c1, and we wish to apply an additional rotation c2, then we can combine these rotations by multiplying these complex numbers giving a new orientation: c1*c2.
If we are representing a pure rotation then the complex number is usually unit length, we say that it is normalised, (real)2 + (imaginary)2 =1
to normalise a complex number calculate:
1/√((real)2 + (imaginary)2)
and multiply this by both real and imaginary parts.
Transformations using complex numbers
type |
formula |
where: |
| transform a point | Pout = Pin * C |
|
| rotations | CR = C1 * C2 |
|
| representing parallel projection | (ac + bd)(c+d i)/√(a2 + b 2) |
|
| representing perpendicular projection | (ac - bd)(c - d i)/√(a2 + b 2) | |
| reflections | a*(c2 + 2cd(b/a) + d2) + b i*(d2 + 2cd(a/b) + c 2) |
|
| scaling | a*s + b*s i |
|
Alternative representation of rotation using complex numbers (spinor representation)
In many cases the above representation of 2D rotation is the simplest and easiest. However there are more advanced applications where another way is useful. The advantages of this method are:
- can represent spinors in 2D (is isomorphic to 2D spinors)
- similar to the way that spinors work in 3D
- may not need to use atan2, asin or acos could be used.
This represents rotation as follows:
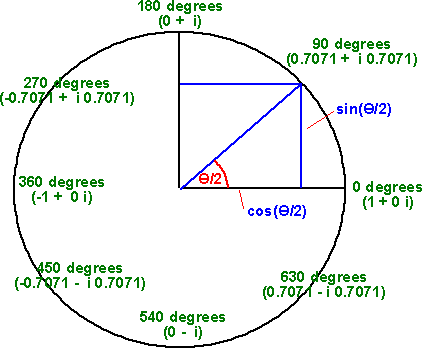
This used angle/2 instead of angle which means that we only need to use quadrants 1 and 2 to encode all the angles between 0° and 360° we could consider the other two quadrants as repeating these angles.
So if we transform a point using the same formula as before:
Pout = Pin * C
Then we rotate the point by half the angle. To transform the point by the required angle then we need to apply it twice:
Pout = Pin * C2
Since complex number multiplications are commutative we can change the order of the operands, for instance we can write this as:
Pout = C * Pin * C
this form emphasizes the similarity to the quaternion equivalent (quaternion transforms explained on this page)
Pout = Q * Pin * Q'
Note: the differences between complex number and quaternion transforms:
| no conjugate of 2nd operand | conjugate of 2nd operand | |
| complex numbers - 2D | Pout = C * Pin * C 2D rotation |
Pout = C * Pin * C' 2D scaling |
| quaternion - 3D | Pout = Q * Pin * Q 3D reflection |
Pout = Q * Pin * Q' 3D rotation |
I would be interested if anyone can see a further pattern here? or can anyone explain these differences? Quaternions have different properties (non-commutative) does that explain these differences?
Overview
The set of all complex numbers is a two dimensional plane which contains the real numbers, shown below as a horizontal line, and the imaginary numbers, shown below as a vertical line.
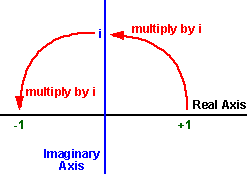
So multiplying by 'i' rotates round to the imaginary axis, and multiplying by 'i' again rotates to the negative real axis. So, i*i=-1, which is just another way of saying that i is the square root of minus one. Therefore the square root of a negative number always has a solution when we are working in complex numbers even though it does not have a solution when we are working purely in real numbers.
Representing Rotations using complex numbers
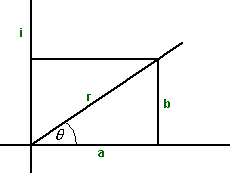
instead of a + i b the complex number could also be represented in what is known as the polar form:
r (cos(θ) + i sin(θ))
in other words replace:
- a = r cos(θ)
- b =r sin(θ)
we can use ei θ = cos(θ) + i sin(θ) to give the exponential form:
r ei θ
If we want combine the result of two rotations, for example rotate by θ1 then rotate by θ2, then we multiply the corresponding complex numbers because:
ei (θ1+θ2) = ei θ1 * ei θ2
Or to combine two rotations by addition if we add the logarithms of the complex numbers.
Demoivre's Theorem
(cos θ + i sin θ)n = cos(n θ) + i sin(n θ)
Since we use multiplication to represent composition of rotations then, we can't use multiplication to represent repeating a rotation 'n' times, instead raising to the power n repeats a rotation 'n' times.
Applications of complex numbers
A complex number could be used to represent the position of an object in a two dimensional plane, complex numbers could also represent other quantities in two dimensions like displacements, velocity, acceleration, momentum, etc. But do the usual equations of motion work correctly?
There does not seem to be any problem with F = m a
where F and a are complex numbers
and m is a scalar.
But we could have done this just as well with a 2 dimensional vector. To really use complex algebra we would need something that in involved multiplication of two complex numbers. I don't think we can use energy equations because energy is a scalar quantity, isn't it?
Another possibility to use complex numbers in simple mechanics might be to use them to represent rotations. We have seen above how complex numbers can be used to represent rotations, but what is the advantage of doing this? why use a complex number when only a single number is needed to represent a rotation angle in a two dimensional plane?
Is there any advantages in using complex numbers to represent the complete state of a solid object, in other words it has a state variable that includes both the position. I don't think this would work because, if we want to combine translations then we add them, but it we want to combine rotations using complex numbers then we multiply them. So we cant combine operations using a single operation. We would be better off using a 3 element vector, two elements for position and one for orientation angle.
There are a lot of applications in physics and engineering where complex numbers are useful.
A common use of complex numbers is in electrical circuits, where capacitors and inductors are like an imaginary component of resistors. This only applies when using alternating current at the frequency being used. In other words, if the frequency of the current changes then the complex 'resistance' value of the components will very. This type of analysis could also be applied to a mechanical analog of electrical circuits, the spring, mass, damper model. If we want to determine the response of such a model at a particular frequency, then complex numbers would be a good way to do this.
Another use of complex numbers is for generating fractal patterns on a 2-dimentional plane.
Further Pages on this site
Here are some possible ways to take the subject further :
- Quaternions - We can extend these ideas to work in 3 dimensions
- Dual Complex Numbers - Here is a possible way to combine 2D rotations with displacement (linear movement) using a single multiplication operation.
- Car Racing Game - We can use complex numbers to make a car racing game


