On the previous page (here) we derived all possible topologies on a finite labeled set. However many of those topologies are isomorphic to each other, so how can we derive just the topologies which are distinct (not isomorphic to each other)?
I would like to be able to calculate these efficiently, so ideally I would like to find a representation which automatically codes isomorphic topologies as the same representation. So they may not be represented as finite sets as in Birkhoff's representation theorem.
One way to start thinking about this might be: instead of decomposing a labeled set like,
[1,2,3]
What would happen if we decompose an unlabeled set like,
[*,*,*]
| So can we replace the lattice with a linear sequence? | 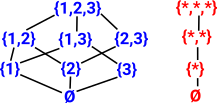 |
This appears to work but when we try to generate all inequivalent topologies, for 3 elements, this would only give us 8 but there should really be 9.
| Labeled Set (29) | (mostly) Unlabeled Set (9) | Shape |
|---|---|---|
| topology=[] | topology=[] | |
| topology=[{1}] topology=[{2}] topology=[{3}] |
topology=[{*}] | |
| topology=[{1, 2}] topology=[{1, 3}] topology=[{2, 3}] |
topology=[{*, *}] | |
| topology=[{1, 2}, {3}] topology=[{2, 3}, {1}] topology=[{1, 3}, {2}] |
topology=[{*, *}, {#}] | |
| topology=[{1, 2}, {1}] topology=[{1, 3}, {1}] topology=[{1, 2}, {2}] topology=[{2, 3}, {2}] topology=[{1, 3}, {3}] topology=[{2, 3}, {3}] |
topology=[{*, #}, {#}] | |
| topology=[{1, 2}, {1}, {2}] topology=[{1, 3}, {1}, {3}] topology=[{2, 3}, {2}, {3}] |
topology=[{*, *}, {*}, {*}] | |
| topology=[{1, 2}, {1, 3}, {1}] topology=[{1, 2}, {2, 3}, {2}] topology=[{1, 3}, {2, 3}, {3}] |
topology=[{*, *}, {*, *}, {*}] | |
| topology=[{1, 2}, {1, 3}, {1}, {2}] topology=[{1, 2}, {2, 3}, {1}, {2}] topology=[{1, 2}, {1, 3}, {1}, {3}] topology=[{1, 3}, {2, 3}, {1}, {3}] topology=[{1, 2}, {2, 3}, {2}, {3}] topology=[{1, 3}, {2, 3}, {2}, {3}] |
topology=[{*, *}, {*, *}, {*}, {*}] | |
| topology=[{1, 2}, {1, 3}, {2, 3}, {1}, {2}, {3}] | topology=[{*, *}, {*, *}, {*, *}, {*}, {*}, {*}] |
This is because if we have a 1 element open set {1} and a two element open set {1,2} there are two possibilities:
| [{1},{1,2}] | the open sets share a common element (one is a subset of the other) | |
| [{1},{2,3}] | the open sets don't share a common element (no subset) |
So do we need to put some labeling back it so that we can distinguish between these two cases? Or can we include the subset relationship as part of the representation?
| That is: | is different than this: | 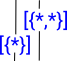 |
So the structure is looking like a partial order.
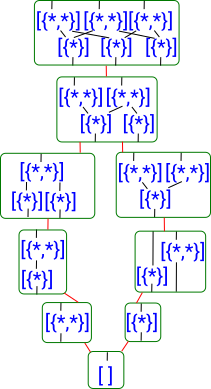 |
4 Element Set
If we move up to the 4 element inequivalent finite set then there are even more complications.
In order to study this I will try to use the same approach as before and look at each grade separately.
Start with finding all topologies that have one singleton {1}.
Look for all possible 2-element sets that could go with it. (here I have gone back to labeling the elements of the open sets, but only as representatives of isomorphic classes) |
 |
The case shown in red is not valid because in a 4-element set we can't have 5 elements. So this is the first restriction on possible topology classes. If:
- 'a' is the number of singletons.
- 'b' is the number of 2-element sets.
- 'c' is the number of subset relations.
- 'n' is the total number of elements in top.
Then n >= a + 2*b - c
Now move on to finding all topologies that have two singletons {1} {2}
Again look for all possible possible 2-element sets that could go with them. There must always be a {1 ,2} set due to the join requirement. Of course all sets join at the top set (not shown on these diagrams) but they must join where there are not additional elements. So the case outlined in red is not valid. |
 |
Now move on to finding all topologies that have 3 singletons.
This illustrates another invalid case, this time due to the meet requirement. |
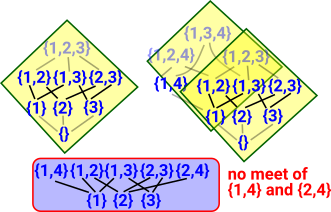 |
Grade 0With no open sets of degree 2: |
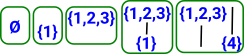 |
Grade 1
With one open set of degree 2:
This gives 16 inequivalent combinations.
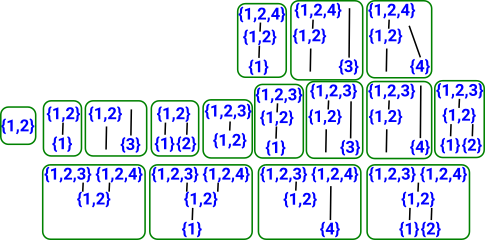
Grade 2
With two open sets of degree 2:
This gives 7 inequivalent combinations.
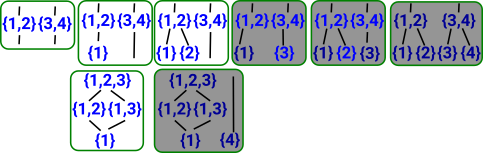
Grade 3With 3 sets of degree 2: |
 |
Grade 4With 4 sets of degree 2: |
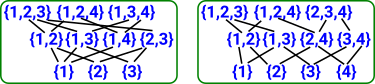 |
Grade 5
With 5 open sets of degree 2 there are not any valid combinations.
Grade 6With 6 sets of degree 2 the only valid combination is the discrete topology. |
 |
