I am looking for an efficient way to represent a topology, one possibility is to build a big topology from smaller discrete topologies.
Category Theory Principles
Let 'Topol' be all topologies on a finite set of a given size. For example Topol(5) could be a category of all topologies in a 5 element set. Let exten: Topol(5)->Topol(5) be an endofunctor from this category to itself. These endofunctors are characterised as functors which increase the number of elements so I have called them 'extensions'. |
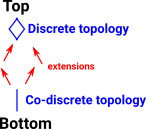 |
Therefore, if we apply these extensions, we move from bottom to top. By composing these extensions we always get to top eventually.
This is equivalent to the other way to enumerate topologies (see Yoneda lemma).
As Monad
In order to compute these topologies it is useful to package them in a monad.
The monad is the above endofunctor with two natural transformations:
- The unit (or return operation)
- The multiplication (sometimes called join operation but it would be confusing to use that name here) which corresponds to composing the extensions.
Practice
Do we need to glue them together using common labels or can we find some method without the need to define labels?
As an example imagine we have a topology: [{},{A},{B},{A,B},{B,C},{A,B,C}] A possible sub-topology (shown in green) would be: [{},{A},{B},{A,B}] Another sub-topology (shown in yellow) would be: [{B},{A,B},{B,C},{A,B,C}] but only after factoring out the common element 'B': {B}*[{},{A},{C},{A,C}] |
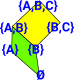
In this diagram the points are open sets and the faces are sub-topologies. These points/open-sets form a lattice. |
Internal Algebra of Lattice
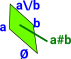
In order to compute with this I am trying to invent an internal algebra of lattices. So I will choose '#' as an operator symbol to construct a lattice on a two element set {a,b}:
a # b = 0 + a + b + a\/b |
 |
So here are some operations in this algebra:
| operator | Internal Algebra of Lattice | As Set of Sets | meaning |
|---|---|---|---|
| # | Construct a complete lattice: a # b = 0 + a + b + a\/b |
{{},{a},{b},{a,b}} = powerset P{a,b} |
I think of this as being all paths from 0 to a\/b. We could go via 'a' or via 'b' or direct to 'a\/b'. |
| \/ | Join: a \/ b |
{a,b} union |
I think of this as going directly from 0 to a\/b |
| /\ | Meet | {a,b} /\ {b,c} = {b} intersection |
|
| + | Glue two lattices together. a+a = a Where the same element occurs in different lattices this gues them together. |
||
| 0 | bottom element On its own, this is not a complete lattice. |
empty set {} |
|
| 1 | top element | whole set {a,b,c} |
|
| c\/(a # b) | Factor out a common element of a lattice: c\/(a # b) = c+ a\/c + b\/c + a\/b\/c |
{c} \/ {{},{a},{b},{a,b}} = {{c},{a,c},{b,c},{a,b,c}} |
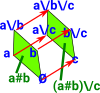 |
| c#(a\/b) |
c#(a\/b) |
{{},{c},{a,b},{a,b,c}} | 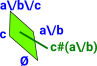 |
So lets try to construct a lattice on a three element set {a,b,c} by expanding out a lattice of a lattice:
(a # b) # c = ( 0 + a + b + a\/b) # c
= 0 + ( 0 + a + b + a\/b) + c + ( 0 + a + b + a\/b) \/ c
In order to expand out the last term we need to use a distributive law for the '+' and '\/' operations.
= 0 + 0 + a + b + a\/b + c + 0\/c + a\/c + b\/c + a\/b\/c
What is 0\/c ? In set terms we are doing a join to an empty set so:
0\/c = c
This gives us two copies of 'c' so let c+c = c.
So this gives us the powerset on 3 elements:
a # b # c = 0 + a + b + a\/b + c + a\/c + b\/c + a\/b\/c
Computing with these Lattices
I find it most efficien for complete lattices to be specified by basis nodes. That is the elements of the lattice may be specified either directly by a number such as '1' (basis node) or other nodes are only implied by a requirment of a join of multiple numbers such as '1\/2\/3'.
Lattice as Union of Power Sets
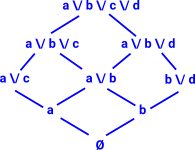 |
The lattice shown here is not a powerset but can it be made up of multiple powersets? can every lattice be embedded into P(A) for some set A Lattices do not distribute over powerset |
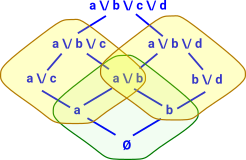
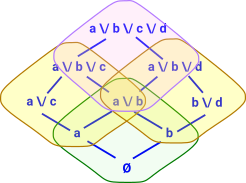
We can start with a powerset based at the bottom element Ø. We can specify it competely by giving the basis elements 'a' and 'b'. Now can we add more powersets so that they cover the entire lattice? |
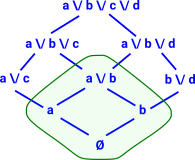 |
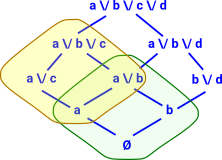 |
I am trying to add more powersets so that their join covers the whole lattice. Note that the join of two powersets is not itself a powerset. Here I have added the yellow powerset. This has bottom at 'a'. To specify this powerset we need to give the basis elements 'b' and 'c' in addition to the bottom element 'a' which is in all the elements (it is like an offset). |
 |
 |
Extending Sub-Topologies
Existing Powerset P(1,2) |
Extension | New Powersets | |
|---|---|---|---|
| [1] -> [[3]] |  |
1*P(2,3) | |
| [1] -> [[3,4]] |  |
1*P(2,[3,4]) | |
| [1] -> [[3],[4]] | 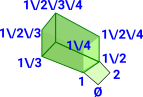 |
1*P(2,3,4) | |
| [1,2] -> [[3]] | (1\/2)*P(3) |
Calculating all Topologies
On the page here we looked at a method of generating all topologies on a given set, this was:
- Take all possible combinations of the elements of that set to give a lattice containing all possible open sets.
- Then take all possible combinations of these open sets to give a lattice containing all potential topologies.
So this gave a powerset of a powerset, as we saw this composition of powersets did not combine to give a single complete powerset. However, here I am trying choose subsets where this is possible
so let P be a powerset functor which takes a set to all its subsets. We want a function which takes a composition of powersets to a single complete powerset.
Monads (see page here) are a way to do this sort of composition, this case take:
- f : a -> P b
- g: b -> P c
and get:
- a -> P c
So use a natural transformation, the multiplication operation:
μ : P P -> P
The inner powerset functor has a join operation \/ (which we can think of as a union of sets) and the outer powerset functor has a join operation + (which we can think of as putting the sets side by side).
In order to implement this multiplication operation we need to use the distributive law. This is usually:
(A+B) \/ C = A \/ C + B \/ C
But, in this case the distributive law is not valid so instead we have to use the 'weak distributive law':
(A+B) \/ C = split: (A \/ C + B) , (B \/ C + A)
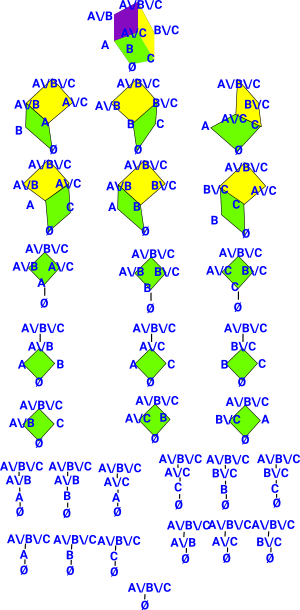
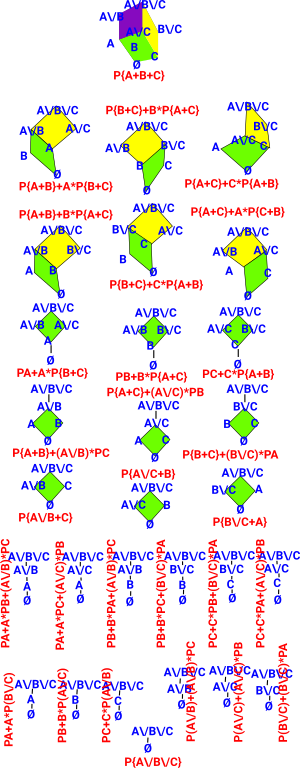
As an example consider all the possible 29 topologies on a 3 element set. In the diagram on the right the diamonds (shown as solid colour) represent complete lattices as they have all meets and joins of open sets. The meets and joins of the sub-lattice can be extended to the whole topology, so we can see that it is a sub-topology. The sub-lattices may be at the root of the whole lattice. But the sub-lattices don't have to be at the root in which case the lowest element is included in every element of the sub-lattice. We can also define meets and joins of the sub-topologies themselves, these are only closed for meets so, for whole sub-topologies, it is a MeetSemilattice. Joins of whole sub-topologies are sets of sub-topologies, this is like gluing sub-topologies together. |
 |
Internal Algebra of LatticeI am trying to invent an internal algebra of lattices. So this: [{1, 2, 3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {1, 2}, {1, 3}, {2, 3}, {1, 4}, {1}, {2}, {3}, {}] could be coded like this: P{1, 2, 3}+{1, 4}+{1, 2, 4}+{1, 3, 4}+{1, 2, 3, 4} Where P means powerset. This is the same way that simplicial complexes are coded. A 'discrete' topology corresponds to a 'face' and simplicial complexes are built up from faces. I am not saying that simplicial complexes are the same as these topologies (we know they are not). I am just thinking they might be represented in a similar way. I have not thought through all of this yet, one thing I would like to implement is simplicial sets (simplicial complexes with degenerate faces) Is there any way degenerate faces could be brought into this theory. |
 |
 |
|
|
Unfortunately the usual distributive law does not work instead we have to use the 'weak distributive law' which splits the lattices:
(X+Y) \/ Z = (X \/ Z + Y) + (Y \/ Z + X)
Which is intended to be two lattices (X \/ Z + Y) and (Y \/ Z + X) glued together .
(for justification of this lookup: 'weak distributive law' of powerset monad.) So using this law we get:
= 0 + ( 0 + a + b + a\/b) + c + ( 0 \/ c + a + b + a\/b) + (a \/ c+ b + a\/b) + (b \/ c+ a + a\/b) + (a\/b\/c+ a + b)
This is a complete cover of all terms (multiple times)
[0 , a , b , c , a\/b , a\/c , b\/c , a\/b\/c]
So I assume that a multiple cover does not matter:
a + a = a
Meets of Sub-Topologies
How can we define meets of sub-topologies? For example, if we have: {1}*P{2,3} /\ {3}*P{1,2} where:
we get [{1,3}, {1,2,3}] which I am denoting as {1,3}*P{2} |
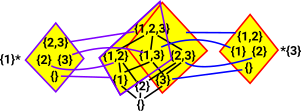 |
So the rules are:
| {a}*P{b,c} /\ {d}*P{e,f} = {} | if the entries are all different then meet is {} |
| {a}*P{b,c} /\ {a}*P{e,f} = {a} | if the offsets are the same but the lattices are different then meet is {a} |
| {a}*P{b,c} /\ {d}*P{b,c} = {} | if the offsets are different but the lattices are the same then meet is {} |
| {a}*P{b,c} /\ {d}*P{a,f} = {} | if the first offset is in the other lattice then meet is {} |
| {a}*P{d,c} /\ {d}*P{a,f} = {a,d} | if each offset is in the other lattice then meet is {a,d} |
| {a}*P{b,c} /\ {a}*P{b,f} = {a} P{b} | if the offsets are the same {a} , the lattices have a common element {b} then meet is {a} P{b} |
| {a}*P{b,c} /\ {a}*P{b,c} = {a}*P{b,c} | if the entries are all the same then meet is same as each operand |
